L'erreur absolue est la différence entre la valeur mesurée et la valeur réelle.[1] C'est une façon de considérer l'erreur lors de la mesure de la précision des valeurs. Si vous connaissez le réel et les valeurs mesurées, le calcul de l'erreur absolue est une simple question de la soustraction. Parfois, cependant, vous pouvez être à côté de la valeur réelle, dans ce cas, vous devez utiliser le maximum d'erreur possible que l'erreur absolue.[2] Si vous connaissez la valeur réelle et le rapport d'erreur, vous pouvez revenir en arrière pour trouver l'erreur absolue.
Mesures
@@_
@@
Méthode 1
à l'Aide de la Valeur Réelle et la Valeur Mesurée

1
@@_
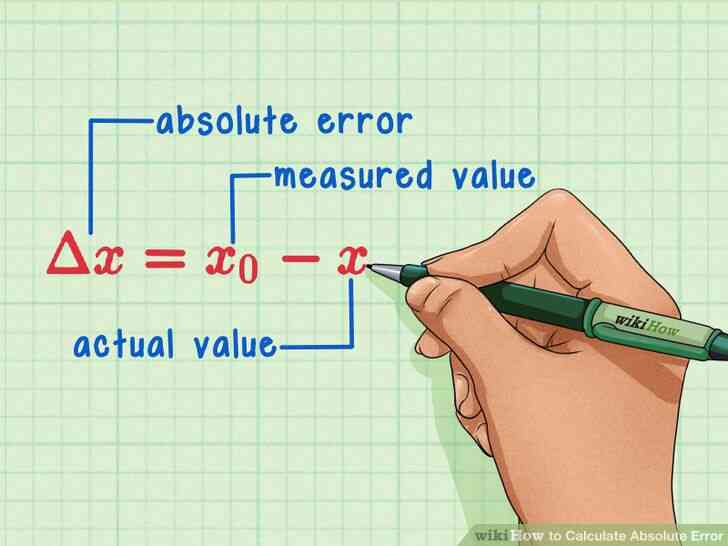
@@configurer la formule pour calculer l'erreur absolue. La formule est ?x=x0-x{\displaystyle \Delta x=x_{0}-x}, où ?x{\displaystyle \Delta x} est égale à l'erreur absolue (la différence, ou de modifier, dans la mesure et la valeur réelle), x0{\displaystyle x_{0}} est égale à la valeur mesurée, et x{\displaystyle x} est égale à la valeur réelle.[3]
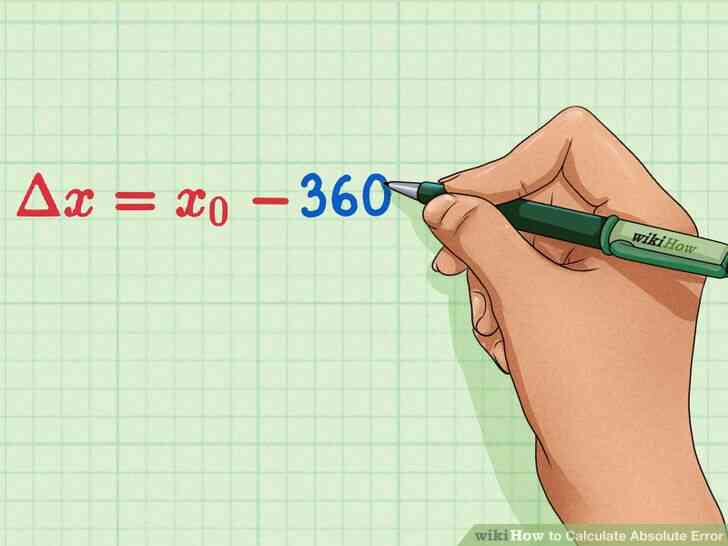
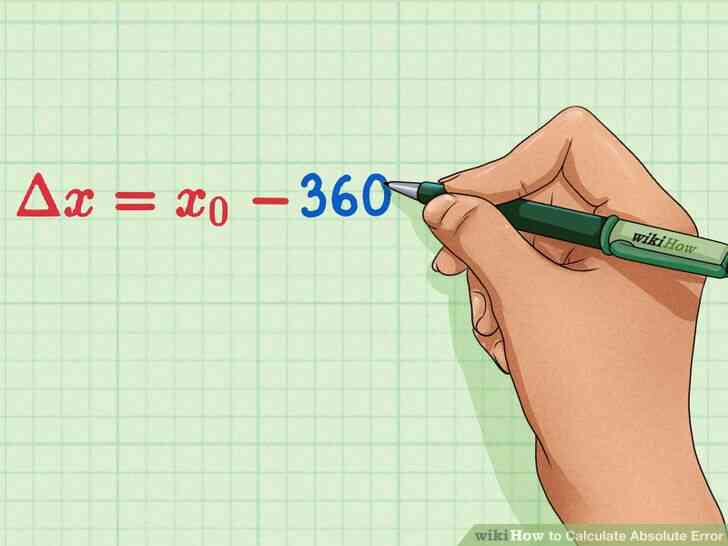
2
@@_
@@Fiche de la valeur réelle dans la formule. La valeur réelle doit être donnée à vous. Sinon, utilisez un standard accepté de valeur. Substituer cette valeur pour x{\displaystyle x}.
- Par exemple, vous pourriez être en mesure de la longueur d'un terrain de football. Vous savez que le réel, ou accepté la longueur d'un professionnel de football Américain de terrain est de 360 pieds. Ainsi, vous souhaitez utiliser 360 que la valeur réelle:?x=x0-360{\displaystyle \Delta x=x_{0}-360}.


3
@@_
@@Trouver la valeur mesurée. Ce sera donnée à vous, ou vous devez prendre les mesures vous-même. Substituer cette valeur de x0{\displaystyle x_{0}}.
- Par exemple, si vous mesurez le terrain de football et de trouver que c'est de 357 mètres de long, vous pouvez utiliser 357 que la valeur mesurée:?x=357-360{\displaystyle \Delta x=357-360}.
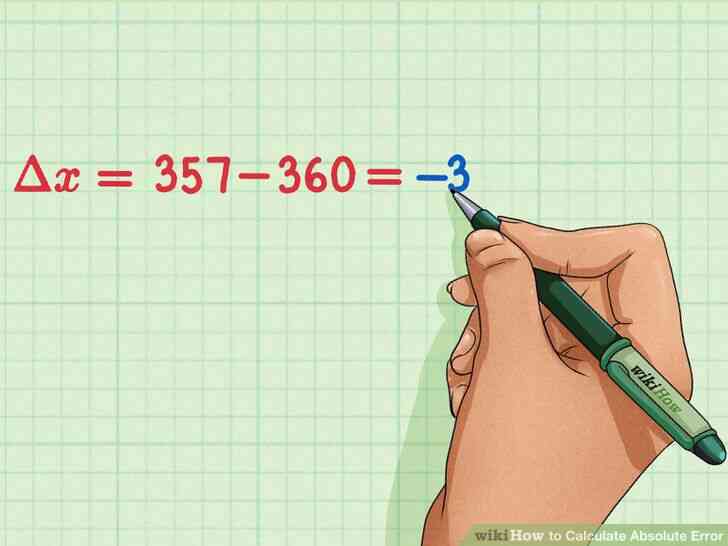
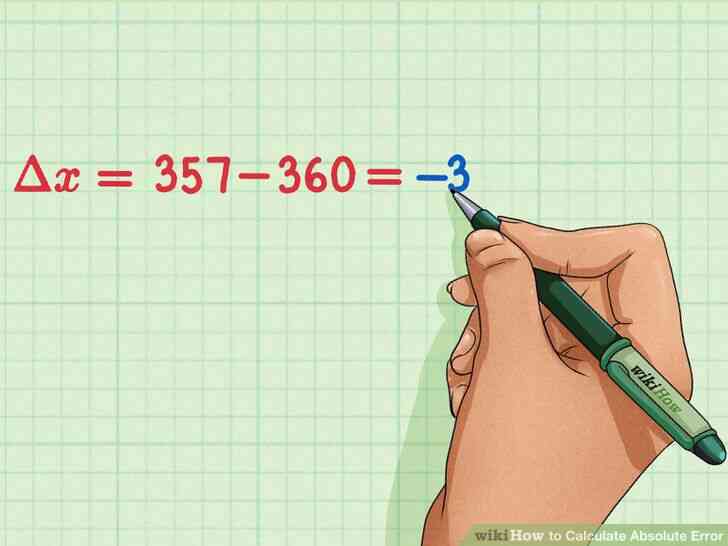
4
@@_
@@Soustraire la valeur réelle de la valeur mesurée. Depuis l'erreur absolue est toujours positive, prendre la valeur absolue de cette différence, en ignorant les signes négatifs.[4] Cela vous donnera l'erreur absolue.
- Par exemple, depuis ?x=357-360=-3{\displaystyle \Delta x=357-360=-3}, l'erreur absolue de la mesure est de 3 pieds.
@@_
@@
Méthode 2
à l'Aide de la Valeur Réelle et l'Erreur Relative


1
@@_
@@configurer la formule de l'erreur relative. La formule est dx=x0-xx{\displaystyle \delta x={\frac {x_{0}-x}{x}}}, où dx{\displaystyle \delta x} est égale à l'erreur relative (le ratio de l'erreur absolue à la valeur réelle), x0{\displaystyle x_{0}} est égale à la valeur mesurée, et x{\displaystyle x} est égale à la valeur réelle.[5]
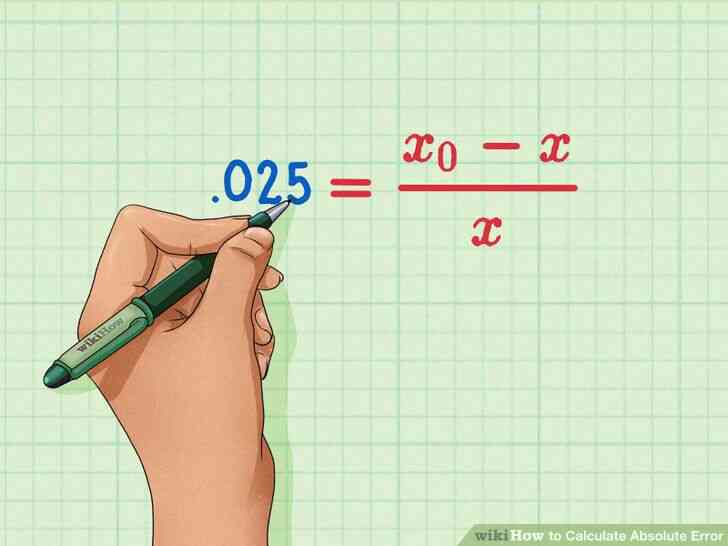
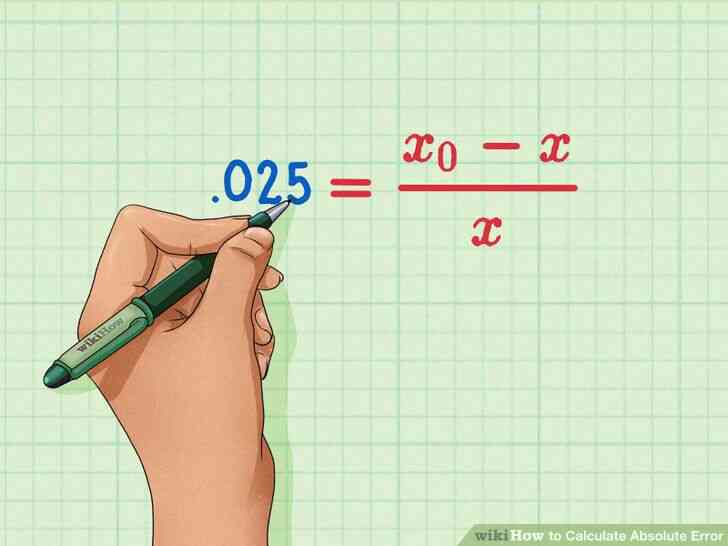
2
@@_
@@Fiche dans la valeur de l'erreur relative. Ce sera probablement une virgule. Assurez-vous de le substituer par dx{\displaystyle \delta x}.
- Par exemple, si vous savez que l'erreur relative est .025, votre formule ressemble à ceci: .025=x0-xx{\displaystyle .025={\frac {x_{0}-x}{x}}}.
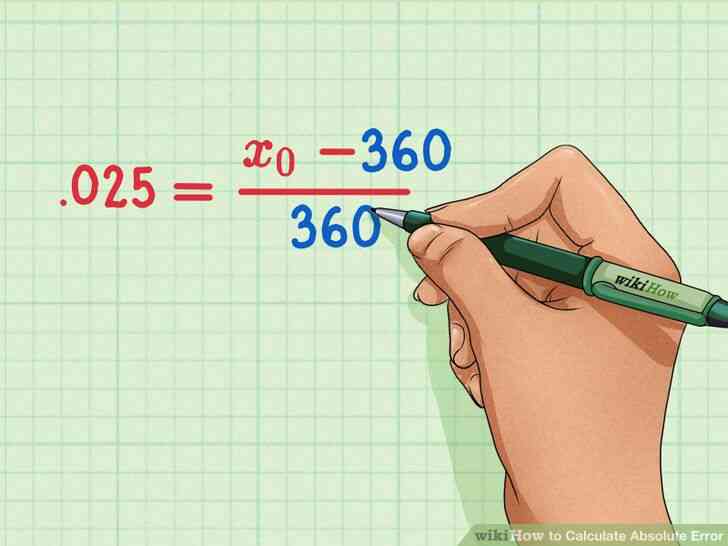
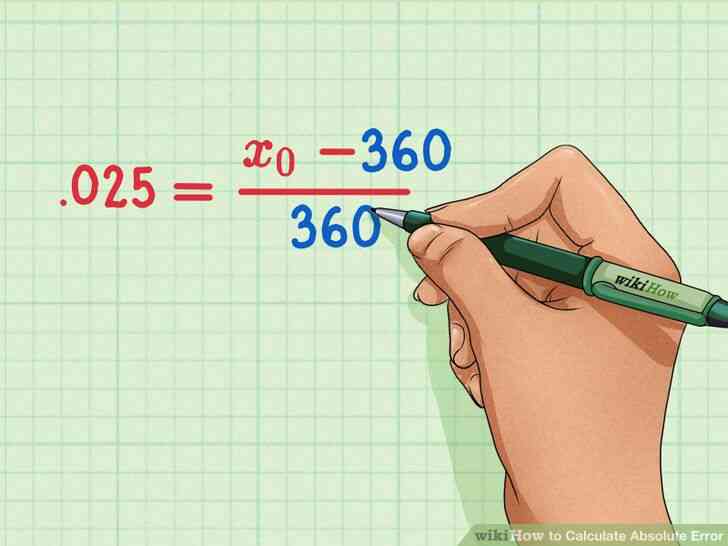
3
@@_
@@Fiche de la valeur pour la valeur réelle. Cette information devrait être donnée à vous. Assurez-vous de remplacer cette valeur pour x{\displaystyle x}.
- Par exemple, si vous savez que la valeur réelle est de 360 ft, votre formule ressemble à ceci: .025=x0-360360{\displaystyle .025={\frac {x_{0}-360}{360}}}.
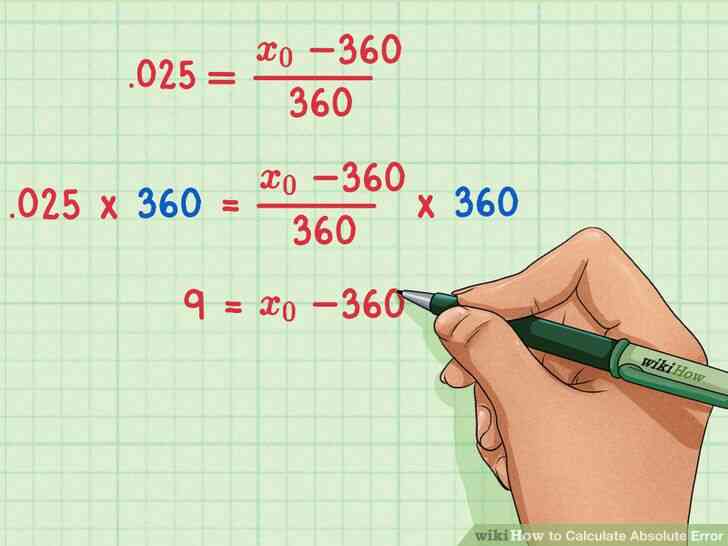
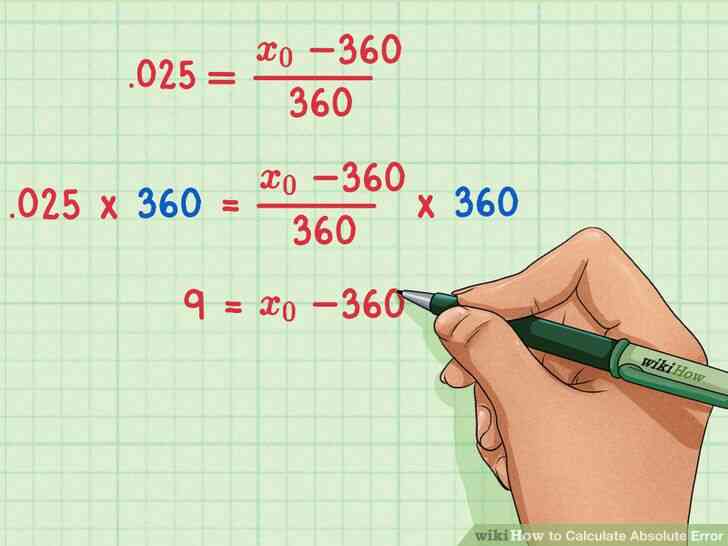
4
@@_
@@Multiplier chaque côté de l'équation par la valeur réelle. Ceci annulera la fraction.
- Par exemple:.025=x0-360360{\displaystyle .025={\frac {x_{0}-360}{360}}}.025×360=x0-360360×360{\displaystyle .025\times 360={\frac {x_{0}-360}{360}}\fois 360}9=x0-360{\displaystyle 9=x_{0}-360}
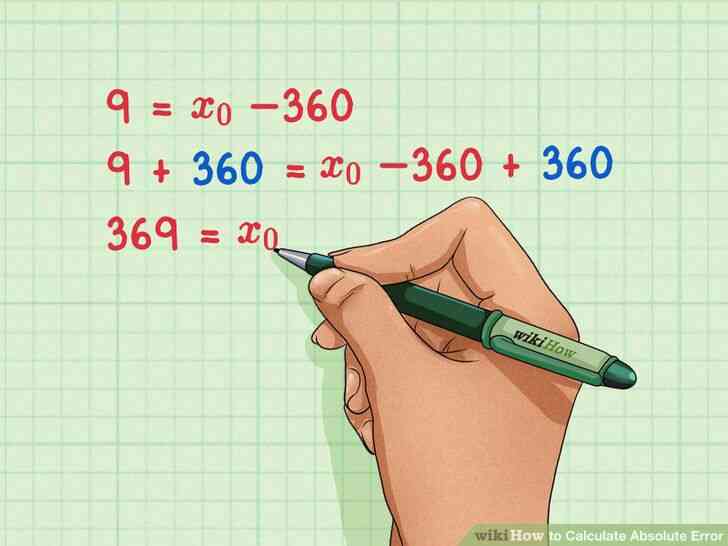
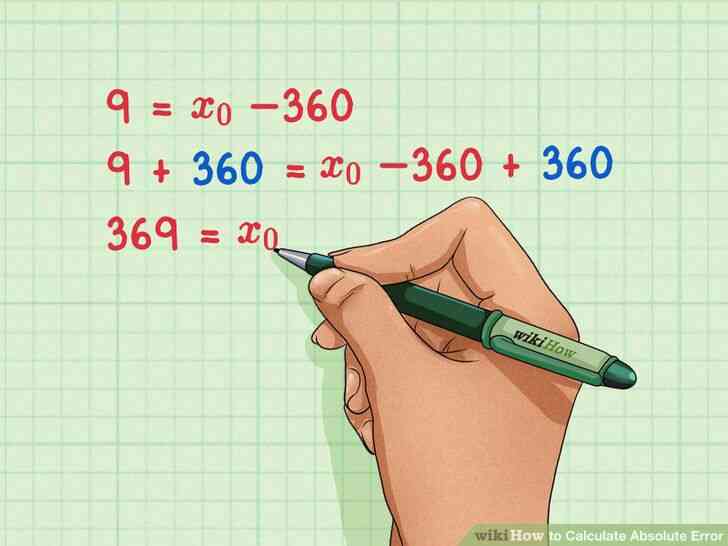
5
@@_
@@Ajouter de la valeur réelle de chaque côté de l'équation. Cela vous donnera la valeur de x0{\displaystyle x_{0}}, vous donnant la valeur mesurée.
- Par exemple:9=x0-360{\displaystyle 9=x_{0}-360}9 360=x0-360 360{\displaystyle 9 360=x_{0}-360 360}369=x0{\displaystyle 369=x_{0}}
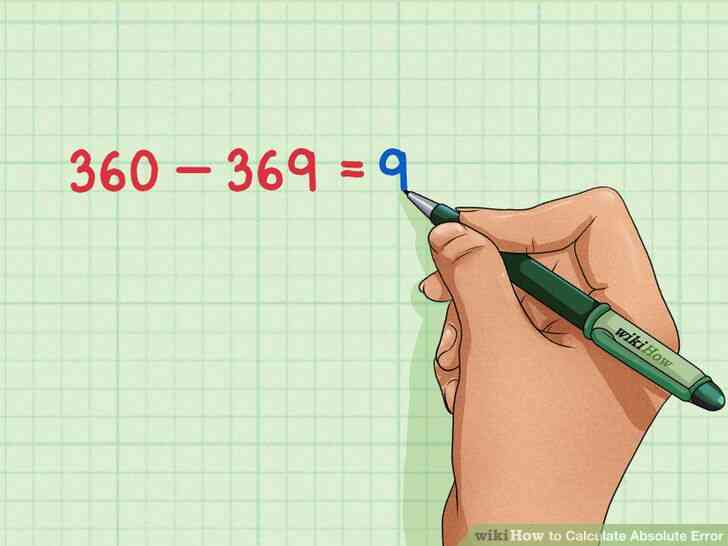
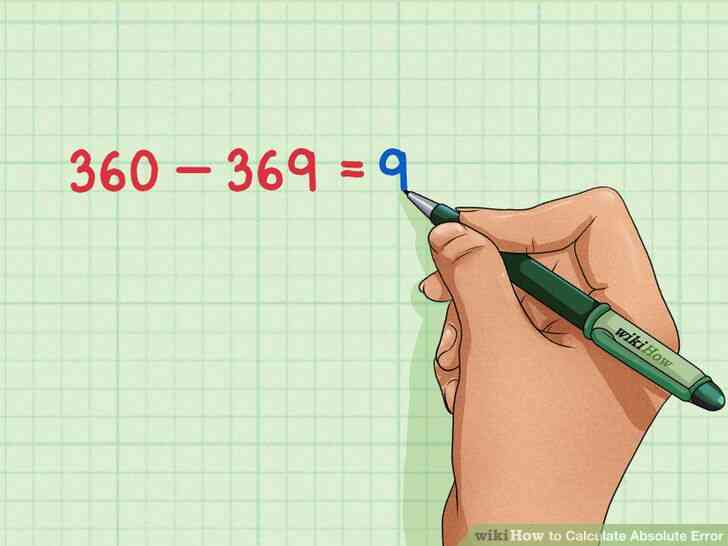
6
@@_
@@Soustraire la valeur réelle de la valeur mesurée. Depuis l'erreur absolue est toujours positive, prendre la valeur absolue de cette différence, en ignorant les signes négatifs.[6] Cela vous donnera l'erreur absolue.
- Par exemple, si la valeur mesurée est de 369 ft, et la valeur réelle est de 360 pieds, vous souhaitez soustraire 369-360=9{\displaystyle 369-360=9}. Donc, l'erreur absolue est de 9 pieds.
@@_
@@
Méthode 3
en Utilisant le Maximum de l'Erreur


1
@@_
@@Déterminer l'unité de mesure. C'est le “au plus proche” de la valeur. Cela peut être déclaré de manière explicite (par exemple, “Le bâtiment a été mesurée la plus proche à pied.”), mais il n'a pas à être. Pour déterminer l'unité de mesure, il suffit de regarder quelle est la place de la valeur de la mesure est arrondie.[7]
- Par exemple, si la longueur mesurée d'un bâtiment est déclaré comme 357 pieds, vous savez que le bâtiment a été mesurée la plus proche à pied. Ainsi, l'unité de mesure est de 1 pied.
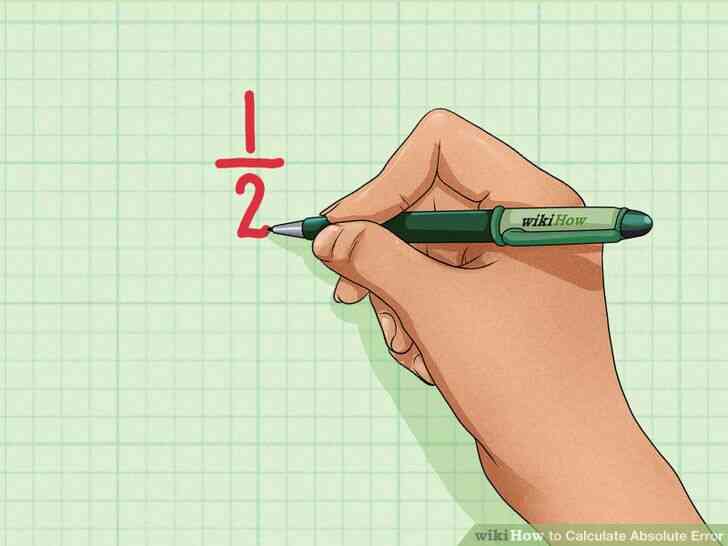
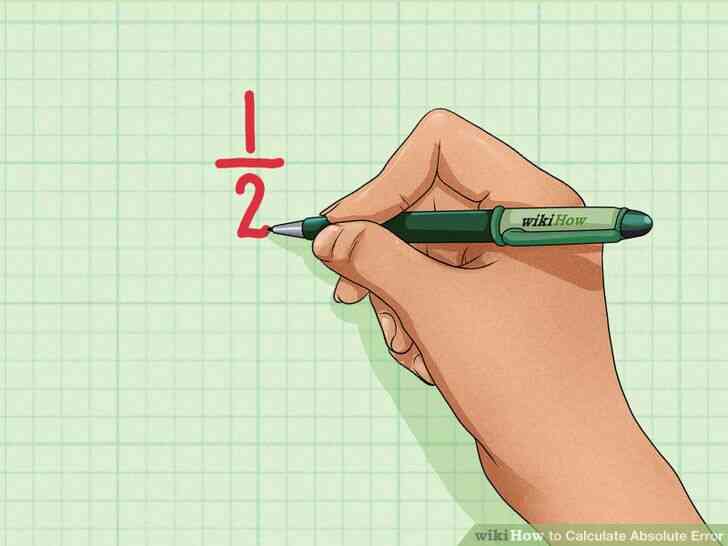
2
@@_
@@Déterminer le nombre maximum d'erreur possible. Le maximum de l'erreur possible est de 12{\displaystyle {\frac {1}{2}}} l'unité de mesure.[8] Vous pouvez voir la liste ±{\displaystyle \h } un certain nombre.
- Par exemple, si l'unité de mesure est un pied, le maximum de l'erreur possible est .5 ft. Donc vous pouvez voir que la mesure d'un bâtiment est de 357±.5 pi{\displaystyle 357\pm .5 pi}. Cela signifie que la valeur réelle de l'immeuble de la longueur pourrait être .5 ft ou moins .5 pieds de plus que la valeur mesurée. Si c'était tout de moins/de plus, la mesure de la valeur aurait été 356 ou 358 pieds.


3
@@_
@@d'Utiliser le maximum d'erreur possible que l'erreur absolue.[9] Puisque l'erreur absolue est toujours positive, prendre la valeur absolue de cette différence, en ignorant les signes négatifs.[10] Cela vous donnera l'erreur absolue.
- Par exemple, si vous trouver la mesure d'un bâtiment à 357±.5 pi{\displaystyle 357\pm .5 pi}, l'erreur absolue est .5 ft.
Comment Calculer l'Erreur Absolue
L'erreur absolue est la difference entre la valeur mesuree et la valeur reelle.[1] C'est une façon de considerer l'erreur lors de la mesure de la precision des valeurs. Si vous connaissez le reel et les valeurs mesurees, le calcul de l'erreur absolue est une simple question de la soustraction. Parfois, cependant, vous pouvez etre a cote de la valeur reelle, dans ce cas, vous devez utiliser le maximum d'erreur possible que l'erreur absolue.[2] Si vous connaissez la valeur reelle et le rapport d'erreur, vous pouvez revenir en arriere pour trouver l'erreur absolue.
Mesures
@@_
@@
Methode 1
a l'Aide de la Valeur Reelle et la Valeur Mesuree


1
@@_
@@configurer la formule pour calculer l'erreur absolue. La formule est ?x=x0-x{\displaystyle \Delta x=x_{0}-x}, ou ?x{\displaystyle \Delta x} est egale a l'erreur absolue (la difference, ou de modifier, dans la mesure et la valeur reelle), x0{\displaystyle x_{0}} est egale a la valeur mesuree, et x{\displaystyle x} est egale a la valeur reelle.[3]
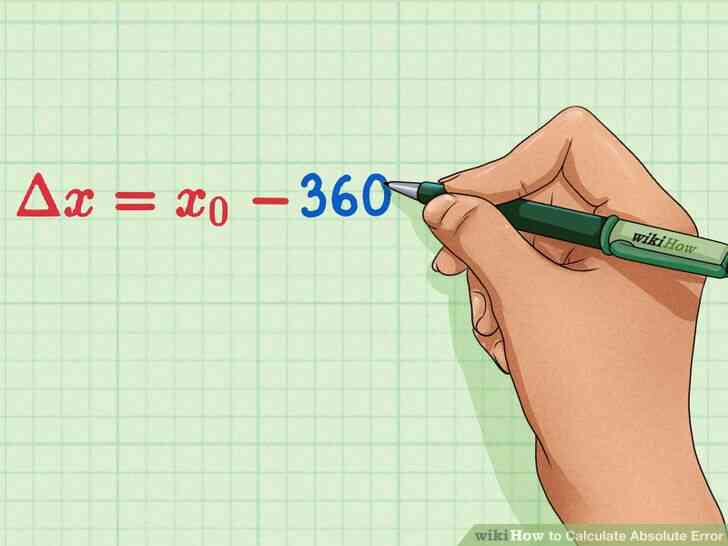
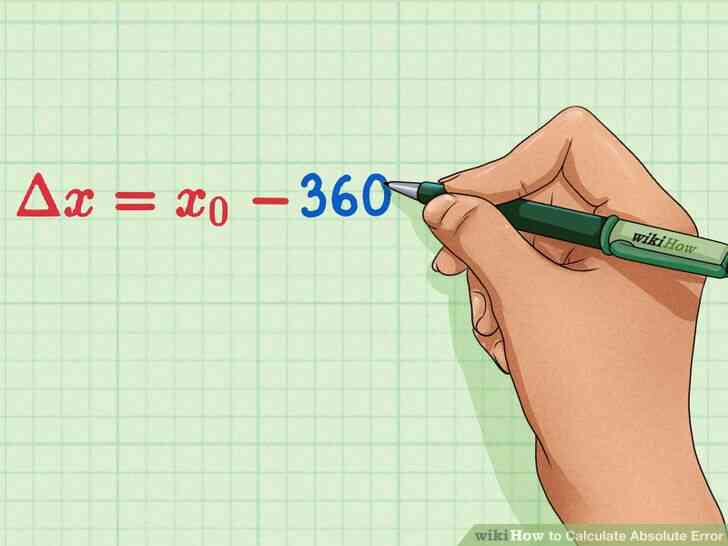
2
@@_
@@Fiche de la valeur reelle dans la formule. La valeur reelle doit etre donnee a vous. Sinon, utilisez un standard accepte de valeur. Substituer cette valeur pour x{\displaystyle x}.
- Par exemple, vous pourriez etre en mesure de la longueur d'un terrain de football. Vous savez que le reel, ou accepte la longueur d'un professionnel de football Americain de terrain est de 360 pieds. Ainsi, vous souhaitez utiliser 360 que la valeur reelle:?x=x0-360{\displaystyle \Delta x=x_{0}-360}.


3
@@_
@@Trouver la valeur mesuree. Ce sera donnee a vous, ou vous devez prendre les mesures vous-meme. Substituer cette valeur de x0{\displaystyle x_{0}}.
- Par exemple, si vous mesurez le terrain de football et de trouver que c'est de 357 metres de long, vous pouvez utiliser 357 que la valeur mesuree:?x=357-360{\displaystyle \Delta x=357-360}.
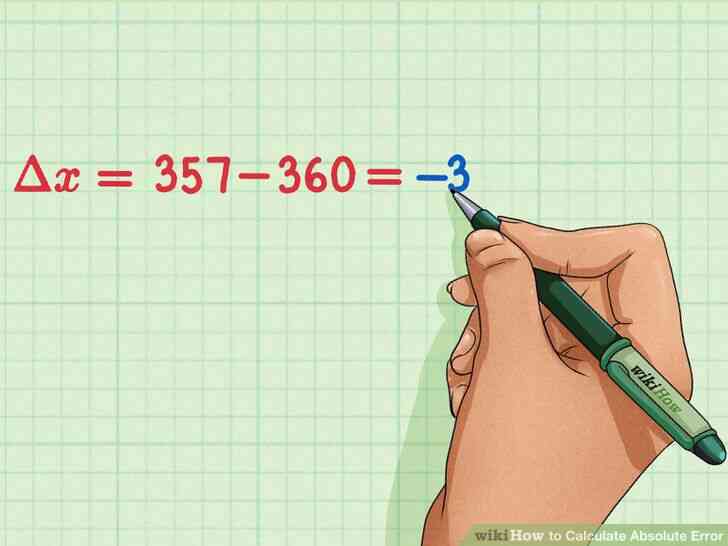
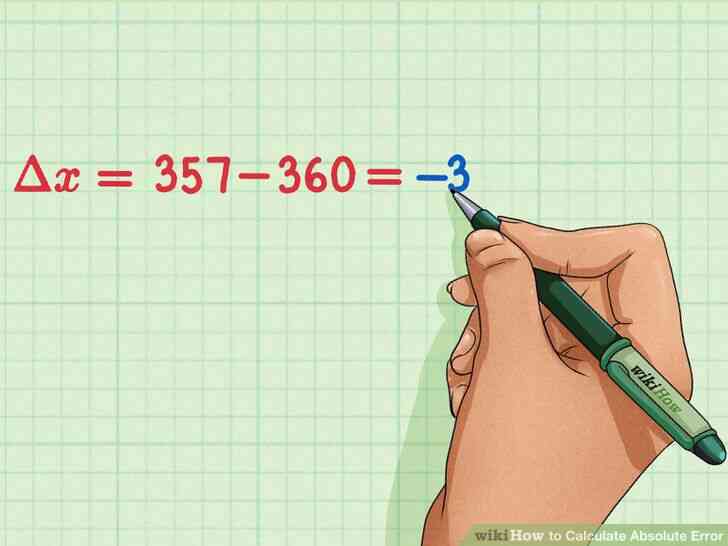
4
@@_
@@Soustraire la valeur reelle de la valeur mesuree. Depuis l'erreur absolue est toujours positive, prendre la valeur absolue de cette difference, en ignorant les signes negatifs.[4] Cela vous donnera l'erreur absolue.
- Par exemple, depuis ?x=357-360=-3{\displaystyle \Delta x=357-360=-3}, l'erreur absolue de la mesure est de 3 pieds.
@@_
@@
Methode 2
a l'Aide de la Valeur Reelle et l'Erreur Relative


1
@@_
@@configurer la formule de l'erreur relative. La formule est dx=x0-xx{\displaystyle \delta x={\frac {x_{0}-x}{x}}}, ou dx{\displaystyle \delta x} est egale a l'erreur relative (le ratio de l'erreur absolue a la valeur reelle), x0{\displaystyle x_{0}} est egale a la valeur mesuree, et x{\displaystyle x} est egale a la valeur reelle.[5]
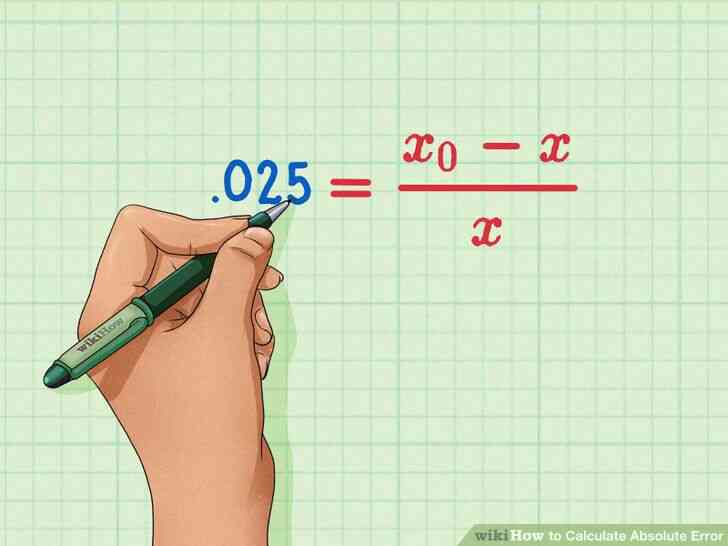
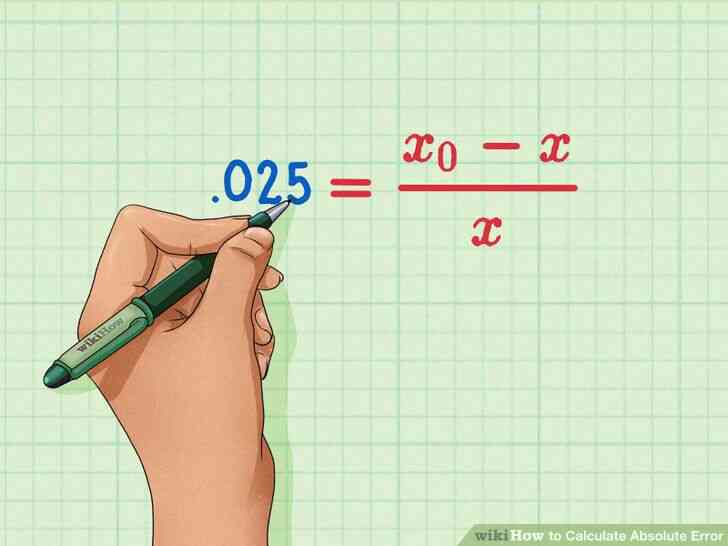
2
@@_
@@Fiche dans la valeur de l'erreur relative. Ce sera probablement une virgule. Assurez-vous de le substituer par dx{\displaystyle \delta x}.
- Par exemple, si vous savez que l'erreur relative est .025, votre formule ressemble a ceci: .025=x0-xx{\displaystyle .025={\frac {x_{0}-x}{x}}}.
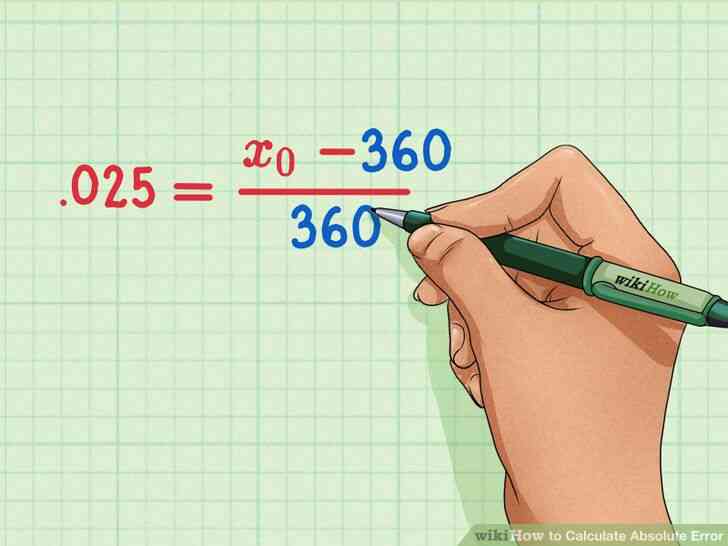
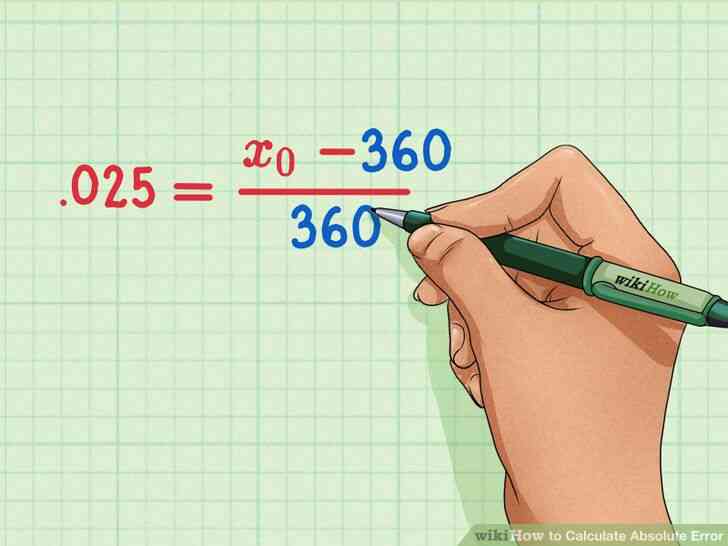
3
@@_
@@Fiche de la valeur pour la valeur reelle. Cette information devrait etre donnee a vous. Assurez-vous de remplacer cette valeur pour x{\displaystyle x}.
- Par exemple, si vous savez que la valeur reelle est de 360 ft, votre formule ressemble a ceci: .025=x0-360360{\displaystyle .025={\frac {x_{0}-360}{360}}}.
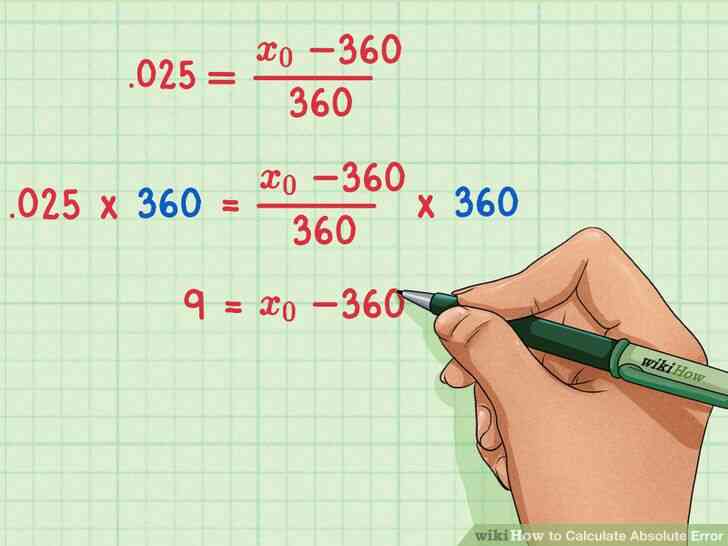
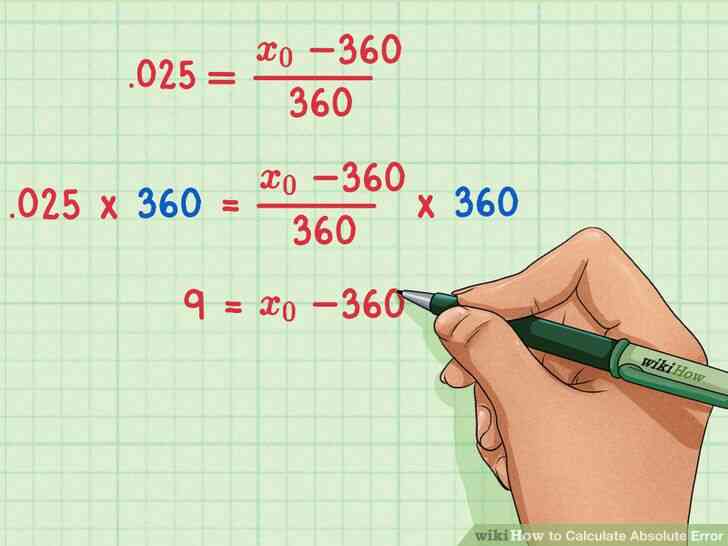
4
@@_
@@Multiplier chaque cote de l'equation par la valeur reelle. Ceci annulera la fraction.
- Par exemple:.025=x0-360360{\displaystyle .025={\frac {x_{0}-360}{360}}}.025×360=x0-360360×360{\displaystyle .025\times 360={\frac {x_{0}-360}{360}}\fois 360}9=x0-360{\displaystyle 9=x_{0}-360}
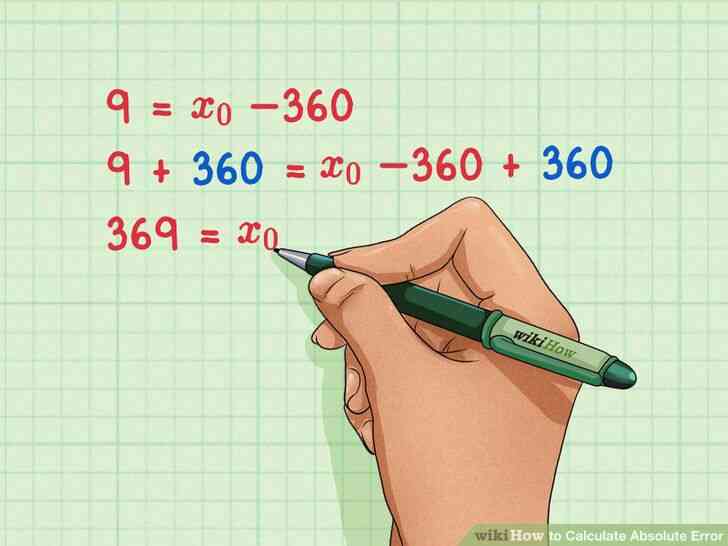
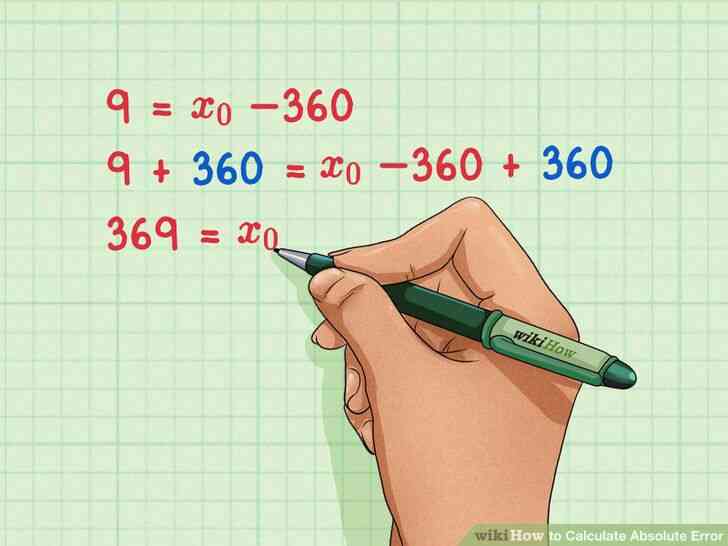
5
@@_
@@Ajouter de la valeur reelle de chaque cote de l'equation. Cela vous donnera la valeur de x0{\displaystyle x_{0}}, vous donnant la valeur mesuree.
- Par exemple:9=x0-360{\displaystyle 9=x_{0}-360}9 360=x0-360 360{\displaystyle 9 360=x_{0}-360 360}369=x0{\displaystyle 369=x_{0}}
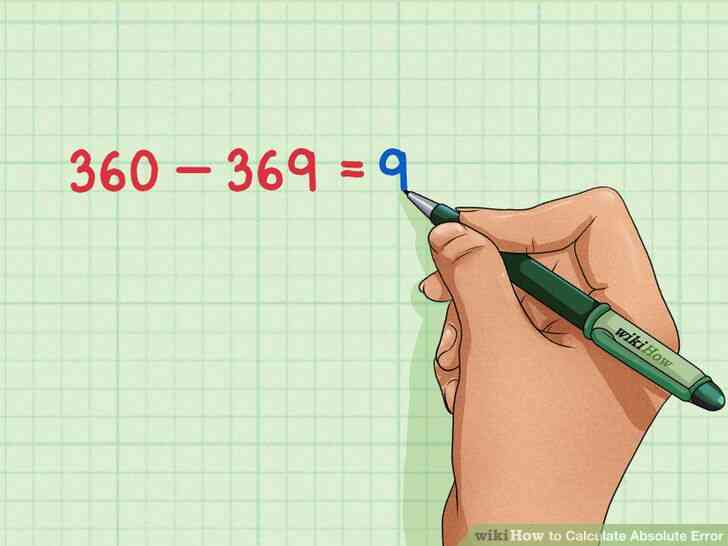
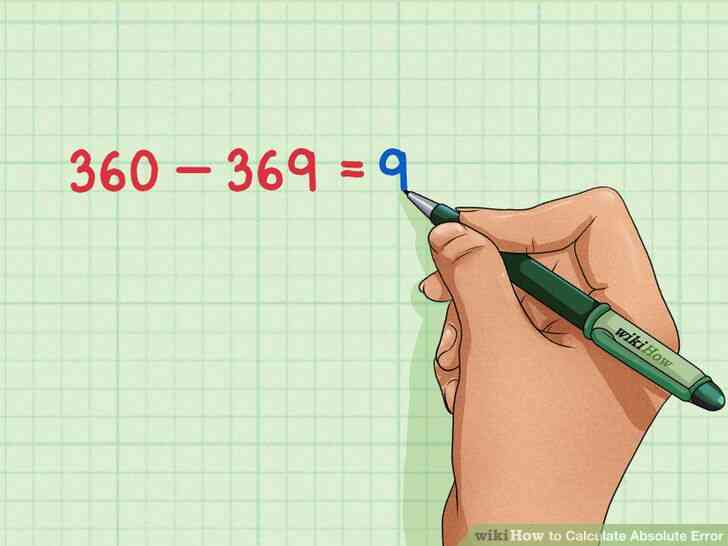
6
@@_
@@Soustraire la valeur reelle de la valeur mesuree. Depuis l'erreur absolue est toujours positive, prendre la valeur absolue de cette difference, en ignorant les signes negatifs.[6] Cela vous donnera l'erreur absolue.
- Par exemple, si la valeur mesuree est de 369 ft, et la valeur reelle est de 360 pieds, vous souhaitez soustraire 369-360=9{\displaystyle 369-360=9}. Donc, l'erreur absolue est de 9 pieds.
@@_
@@
Methode 3
en Utilisant le Maximum de l'Erreur


1
@@_
@@Determiner l'unite de mesure. C'est le “au plus proche” de la valeur. Cela peut etre declare de maniere explicite (par exemple, “Le batiment a ete mesuree la plus proche a pied.”), mais il n'a pas a etre. Pour determiner l'unite de mesure, il suffit de regarder quelle est la place de la valeur de la mesure est arrondie.[7]
- Par exemple, si la longueur mesuree d'un batiment est declare comme 357 pieds, vous savez que le batiment a ete mesuree la plus proche a pied. Ainsi, l'unite de mesure est de 1 pied.
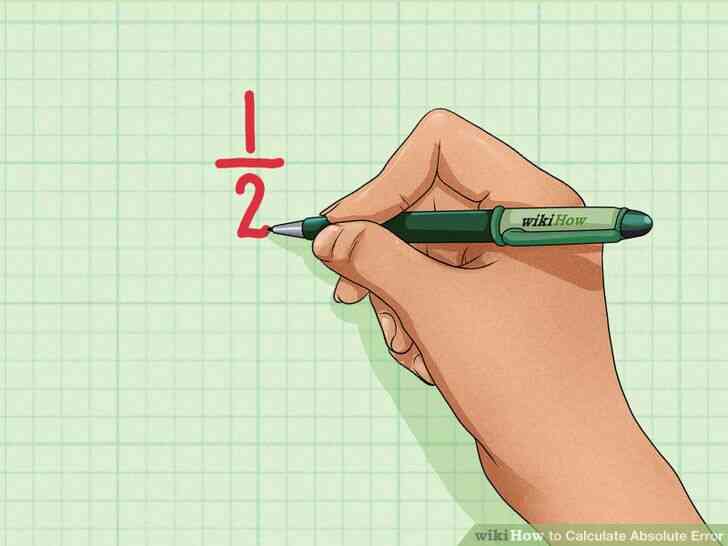
2
@@_
@@Determiner le nombre maximum d'erreur possible. Le maximum de l'erreur possible est de 12{\displaystyle {\frac {1}{2}}} l'unite de mesure.[8] Vous pouvez voir la liste ±{\displaystyle \h } un certain nombre.
- Par exemple, si l'unite de mesure est un pied, le maximum de l'erreur possible est .5 ft. Donc vous pouvez voir que la mesure d'un batiment est de 357±.5 pi{\displaystyle 357\pm .5 pi}. Cela signifie que la valeur reelle de l'immeuble de la longueur pourrait etre .5 ft ou moins .5 pieds de plus que la valeur mesuree. Si c'etait tout de moins/de plus, la mesure de la valeur aurait ete 356 ou 358 pieds.


3
@@_
@@d'Utiliser le maximum d'erreur possible que l'erreur absolue.[9] Puisque l'erreur absolue est toujours positive, prendre la valeur absolue de cette difference, en ignorant les signes negatifs.[10] Cela vous donnera l'erreur absolue.
- Par exemple, si vous trouver la mesure d'un batiment a 357±.5 pi{\displaystyle 357\pm .5 pi}, l'erreur absolue est .5 ft.
Comment Calculer l'Erreur Absolue
By commentfaire
L'erreur absolue est la différence entre la valeur mesurée et la valeur réelle.[1] C'est une façon de considérer l'erreur lors de la mesure de la précision des valeurs. Si vous connaissez le réel et les valeurs mesurées, le calcul de l'erreur absolue est une simple question de la soustraction. Parfois, cependant, vous pouvez être à côté de la valeur réelle, dans ce cas, vous devez utiliser le maximum d'erreur possible que l'erreur absolue.[2] Si vous connaissez la valeur réelle et le rapport d'erreur, vous pouvez revenir en arrière pour trouver l'erreur absolue.