Les carrés magiques ont gagné en popularité avec l'avènement des mathématiques basés sur des jeux comme le Sudoku. Un carré magique est un arrangement de nombres dans un carré de telle manière que la somme de chaque ligne, colonne et diagonale est un nombre constant, le soi-disant "magique constante." Cet article va vous dire comment résoudre n'importe quel type de carré magique, si impaires, seul paire, ou une double paire.
Mesures
@@_
@@
Méthode 1
Résolution d'une Impaires Carré Magique
1
@@_
@@Calculer la magie constante.[1] Vous pouvez trouver ce numéro en utilisant une simple formule math, où n = le nombre de lignes ou de colonnes dans votre carré magique. Ainsi, par exemple, dans un carré magique 3x3, n = 3. La magie constante = n[(n^2 1)/2]. Ainsi, dans l'exemple du carré de 3x3 cases:
- somme = 3 * [(9 1) / 2]
- somme = 3 * (10 / 2)
- somme = 3 * (5)
- somme = 15
- La magie constante pour un carré de 3x3 cases est de 15.
- Toutes les lignes, colonnes et diagonales faut ajouter à ce nombre.


2
@@_
@@Place de numéro 1 dans la boîte de centre sur la ligne du haut. C'est toujours l'endroit où vous commencez quand votre carré magique a impaires côtés, peu importe comment grand ou petit que nombre est. Donc, si vous avez un carré de 3x3 cases, place de numéro 1 dans la Zone 2 dans un carré de 15x15, place de numéro 1 dans la Case 8.

3
@@_
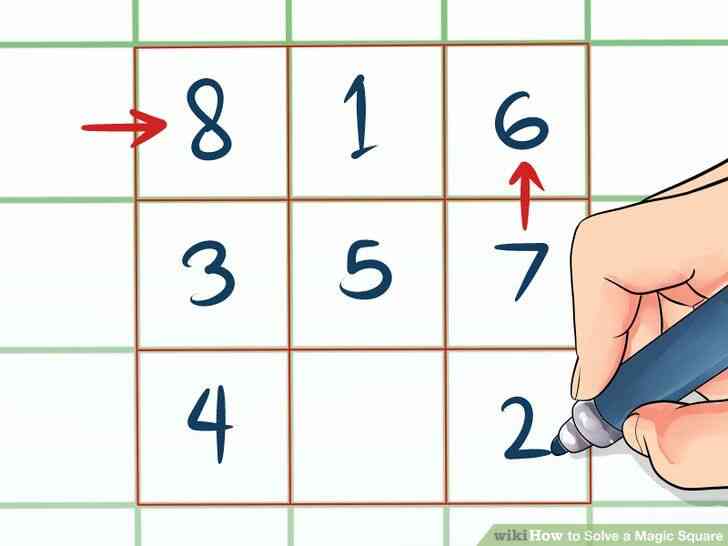
@@Remplir les numéros restants à l'aide d'un-l'un, droit un schéma. Vous aurez toujours remplir les numéros de façon séquentielle (1, 2, 3, 4, etc.) par le déplacement d'une ligne vers le haut, puis une colonne vers la droite. Vous remarquerez immédiatement que, pour placer le numéro 2, vous passerez au-dessus de la rangée du haut, hors du carré magique. Ce n'est pas grave même si vous travaillez toujours dans cette, droite une manière, il y a trois exceptions qui ont également des motifs, prévisible règles:
- Si le mouvement prend de vous une “boîte” au-dessus du carré magique de la rangée du haut, de rester dans la zone de la colonne, mais de placer le numéro de la ligne du bas de la colonne.
- Si le mouvement prend de vous une “boîte” à droite du carré magique de la colonne de droite, rester dans la zone de ligne, mais le nombre le plus à gauche de la colonne de cette ligne.
- Si le mouvement prend de vous une case est déjà occupée, revenir à la dernière case qui a été rempli, et le lieu du prochain numéro directement au-dessous.
@@_
@@
Méthode 2
Résolution d'un Seul Même Carré Magique


1
@@_
@@Comprendre ce qu'est un seul même place. Tout le monde sait qu'un nombre est divisible par 2, mais dans les carrés magiques, il existe différentes méthodes pour résoudre individuellement et doublement même places.
- Une seule encore place a un certain nombre de cases par côté qui est divisible par 2, mais pas 4.[2]
- Le plus petit possible individuellement, même carré magique est 6x6, depuis 2x2 carrés magiques ne peuvent pas être faites.


2
@@_
@@Calculer la magie de la constante. Utilisez la même méthode que vous le feriez avec bizarre carrés magiques: la magie de la constante = [n * (n^2 1)] / 2, où n = le nombre de cases de chaque côté. Ainsi, dans l'exemple d'un carré 6x6:
- somme = [6 * (62 1)] / 2
- somme = [6 * (36 1)] / 2
- somme = (6 * 37) / 2
- somme = 222 / 2
- La magie constante pour un 6x6 carré est 222/2, ou 111.
- Toutes les lignes, colonnes et diagonales faut ajouter à ce nombre.

3
@@_
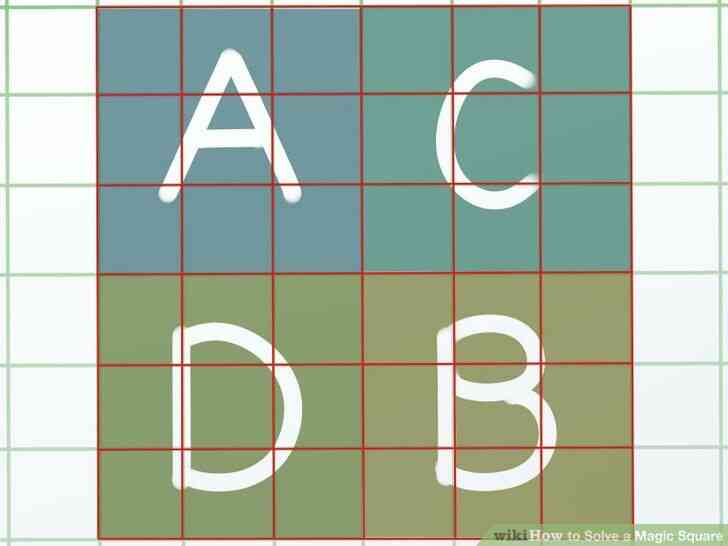
@@Diviser le carré magique en quatre quadrants de taille égale. Étiquette eux Une (en haut à gauche), C (en haut à droite), D (en bas à gauche) et B (en bas à droite). Pour déterminer la taille de chaque carré doit être, il suffit de diviser le nombre de cases dans chaque ligne ou colonne de moitié.
- Donc, pour un 6x6 carré, chaque quadrant de 3x3 cases.


4
@@_
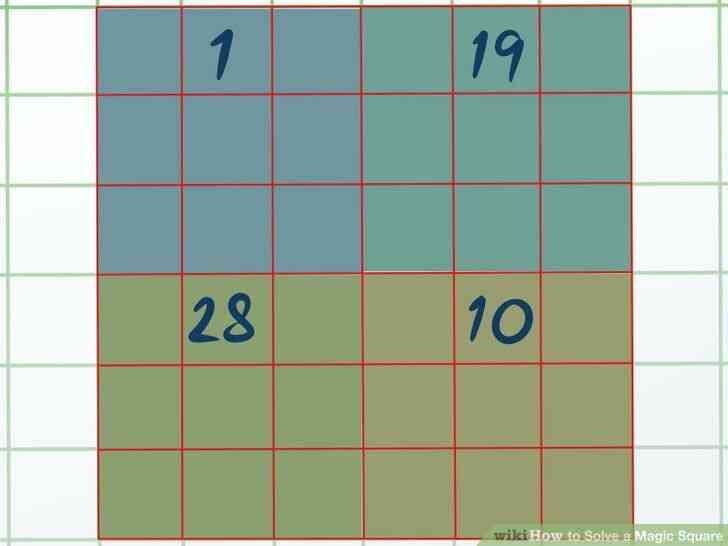
@@Attribuer à chaque quadrant d'un numéro de plage. Quadrant A devient pour le trimestre de nombres Quadrant B du deuxième trimestre Quadrant C le troisième trimestre, et le Quadrant D le dernier quart du nombre total de gamme pour les 6x6 carré magique.
- Dans l'exemple d'un carré 6x6, le Quadrant serait résolu avec les nombres de 1 à 9 Quadrant B avec 10-18 Quadrant C avec 19-27 et le Quadrant D avec 28-36.

5
@@_
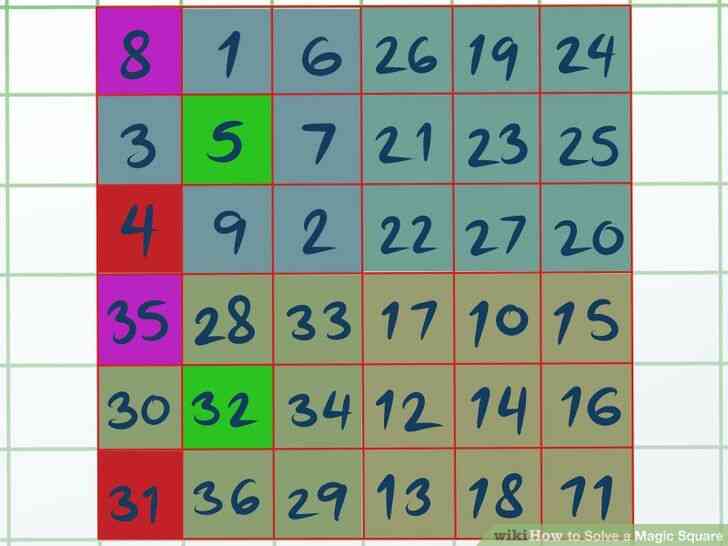
@@Résoudre chaque quadrant à l'aide de la méthodologie pour l'impair, les carrés magiques. Quadrant A sera simple à remplir, car il commence avec le numéro 1, comme les carrés magiques d'habitude. Les Quadrants B-D, cependant, sera de commencer avec des numéros étranges — 10, 19 et 28, respectivement, dans notre exemple.
- Traiter le premier nombre de chaque quadrant, comme si elle est le numéro un. Le placer dans la boîte de centre sur la ligne supérieure de chaque quadrant.
- Traiter chaque quadrant comme son propre carré magique. Même si une case est disponible à côté d'un quadrant, de l'ignorer et passer à la “exception” à la règle qui s'adapte à votre situation.

6
@@_
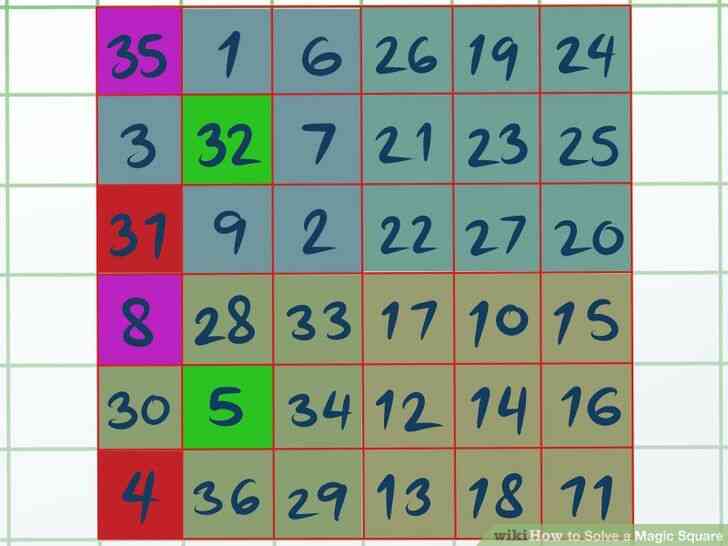
@@Créer des reflets A et D.[3] Si vous avez essayé d'ajouter vos colonnes, les lignes et les diagonales de droite maintenant, vous remarqueriez qu'ils n'ont pas encore ajouter à votre magie constante. Vous avez à échanger quelques cases entre le haut à gauche et en bas à gauche quadrants pour terminer votre carré magique. Nous allons appeler ces échangé des zones de Surbrillance et de mettre en Évidence Un D.
- à l'Aide d'un crayon, marquer toutes les cases de la rangée du haut, jusqu'à ce que vous lisez la médiane de la position de la zone de Quadrant A. Donc, dans un carré 6x6, vous ne cochez la Case 1 (ce qui aurait le nombre de 8), mais dans un carré de 10x10, vous marquez les Cases 1 et 2 (qui aurait les numéros 17 et 24, respectivement).
- Marquer un carré en utilisant les cases vous juste marqué que la ligne du haut. Si vous avez seulement une case, votre place est juste que d'un seul boîtier. Nous allons appeler ce domaine Soulignent Un-1.
- Donc, dans un 10x10 carré magique, mettez en Surbrillance Un-1 serait composé de Cases 1 et 2 dans les Lignes 1 et 2, de la création d'un carré 2x2 en haut à gauche du quadrant.
- Dans la ligne directement en dessous de mettre en Évidence Un-1, ignorez le nombre dans la première colonne, puis cochez autant de cases de l'échelle que vous avez marqué en Évidence Un-1. Nous allons appeler cette ligne du milieu en Évidence Un-2.
- mettre en Évidence Un-3 est une boîte identique à A-1, mais placé dans le coin en bas à gauche du quadrant.
- mettre en Évidence Un-1, A-2 et A-3, ensemble, constituent en Évidence A.
- Répétez ce processus dans le Quadrant D, la création d'un identique zone en surbrillance appelé Highlight D.

7
@@_
@@Swap met en lumière Un et D. C'est un un-à-un swap, il suffit de soulever et de remplacer les cases entre les Quadrants A et Quadrant D sans changer leur ordre. Une fois que vous avez fait cela, toutes les lignes, colonnes et diagonales dans votre carré magique devrait ajouter à la magie de la constante que vous avez calculé.@@_
@@
Méthode 3
Résolution d'un Doublement Même le Carré Magique

1
@@_
@@Comprendre ce qu'est un doublement même place. Une seule encore place a un certain nombre de cases par côté qui est divisible par 2. Un doublement même place a un certain nombre de cases de chaque côté divisible par double — 4.[4]
- Le plus petit doublement la même boîte qui peut être faite est un 4x4 place.


2
@@_
@@Calculer la magie de la constante. Utilisez la même méthode que vous le feriez avec un chiffre impair, soit séparément-même les carrés magiques: la magie de la constante = [n * (n^2 1)] / 2, où n = le nombre de cases de chaque côté. Ainsi, dans l'exemple d'un 4x4 place:
- somme = [4 * (4^2 1)] / 2
- somme = [4 * (16 1)] / 2
- somme = (4 * 17) / 2
- somme = 68 / 2
- La magie constante pour un 4x4 carré est 68/2, ou 34.
- Toutes les lignes, colonnes et diagonales faut ajouter à ce nombre.


3
@@_
@@Créer des reflets A-D. Dans chaque coin du carré magique, de la marque une mini-carré avec des côtés de longueur n/4, où n = la longueur d'un côté de l'ensemble du carré magique.[5] Label met en lumière Une, B, C et D dans le sens antihoraire.
- Dans un 4x4 place, il vous suffit de marquer les quatre coins des boîtes.
- Dans un 8x8 carré, chaque Souligner serait une 2x2 zone dans les coins.
- Dans un carré 12x12, chaque Souligner serait une zone de 3x3 dans les coins, et ainsi de suite.


4
@@_
@@Créer la Centrale de point culminant. Coche toutes les cases dans le centre du carré magique dans une zone carrée de taille n/2, où n = la longueur d'un côté de l'ensemble du carré magique. La Centrale de mettre en Évidence devrait se chevauchent pas avec les faits Saillants de l'A-D, toucher chacun d'entre eux dans les coins.
- Dans un 4x4 carré, la Centrale de mettre en Évidence serait une 2x2 zone dans le centre.
- Dans un 8x8 carré, la Centrale de mettre en Évidence serait un 4x4 de la zone dans le centre, et ainsi de suite.


5
@@_
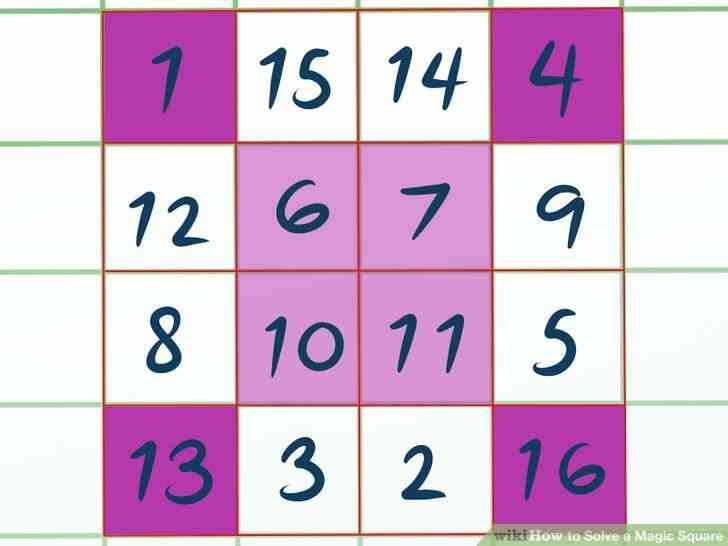
@@Remplir le carré magique, mais seulement dans les zones en Surbrillance. Commencer à remplir les numéros de votre carré magique de gauche à droite, mais seulement écrire le nombre si la boîte de relève d'une Évidence. Donc, dans un 4x4 boîte, vous renseignez les zones suivantes:
- 1 en haut à gauche de la boîte et 4 dans le top-case de droite
- 6 et 7 dans le centre de boîtes dans la Ligne 2
- 10 et 11 dans le centre de boîtes à la Ligne 3
- 13 dans le coin inférieur gauche de la boîte et 16 dans le coin inférieur droit de la boîte.

6
@@_
@@Remplir le reste du carré magique par comptage à rebours. Le est essentiellement l'inverse de l'étape précédente. Recommencer avec la case en haut à gauche, mais cette fois, ignorer toutes les boîtes qui tombent dans la zone en Surbrillance, et remplissez la non-mise en evidence des boîtes par un comptage à rebours. Commencer avec le plus grand nombre dans votre gamme de nombre. Donc, dans un carré magique 4x4, vous remplissez les suivantes:
- 15 et 14 dans le centre de boîtes à la Ligne 1
- 12 dans le menu le plus à gauche et 9 à droite dans la Ligne 2
- 8 dans le menu le plus à gauche et 5 à droite de la boîte dans la Ligne 3
- 3 et 2 dans le centre de cases sur la Ligne 4
- À ce stade, tous vos colonnes, les lignes et les diagonales doivent jusqu'à votre magie constant que vous avez calculé.
Comment Resoudre un Carre Magique
Les carres magiques ont gagne en popularite avec l'avenement des mathematiques bases sur des jeux comme le Sudoku. Un carre magique est un arrangement de nombres dans un carre de telle maniere que la somme de chaque ligne, colonne et diagonale est un nombre constant, le soi-disant "magique constante." Cet article va vous dire comment resoudre n'importe quel type de carre magique, si impaires, seul paire, ou une double paire.
Mesures
@@_
@@
Methode 1
Resolution d'une Impaires Carre Magique
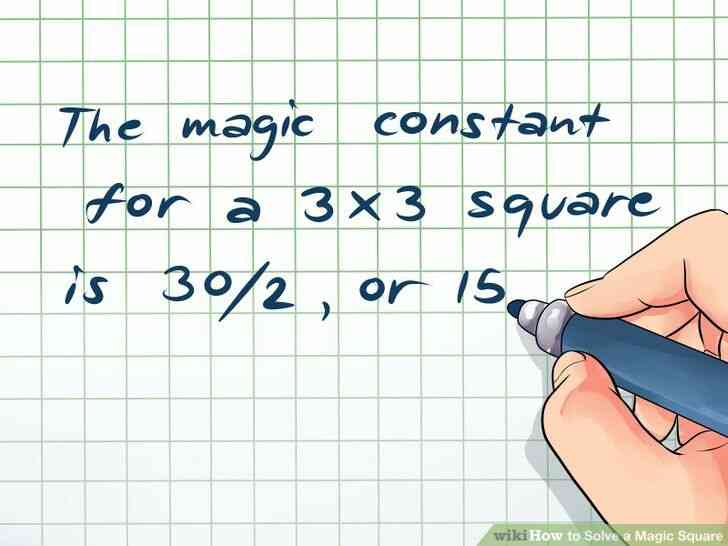
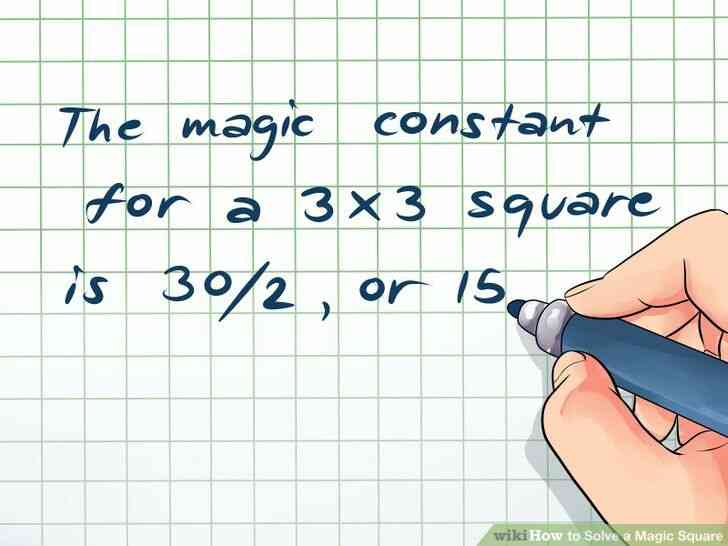
1
@@_
@@Calculer la magie constante.[1] Vous pouvez trouver ce numero en utilisant une simple formule math, ou n = le nombre de lignes ou de colonnes dans votre carre magique. Ainsi, par exemple, dans un carre magique 3x3, n = 3. La magie constante = n[(n^2 1)/2]. Ainsi, dans l'exemple du carre de 3x3 cases:
- somme = 3 * [(9 1) / 2]
- somme = 3 * (10 / 2)
- somme = 3 * (5)
- somme = 15
- La magie constante pour un carre de 3x3 cases est de 15.
- Toutes les lignes, colonnes et diagonales faut ajouter a ce nombre.


2
@@_
@@Place de numero 1 dans la boîte de centre sur la ligne du haut. C'est toujours l'endroit ou vous commencez quand votre carre magique a impaires cotes, peu importe comment grand ou petit que nombre est. Donc, si vous avez un carre de 3x3 cases, place de numero 1 dans la Zone 2 dans un carre de 15x15, place de numero 1 dans la Case 8.


3
@@_
@@Remplir les numeros restants a l'aide d'un-l'un, droit un schema. Vous aurez toujours remplir les numeros de façon sequentielle (1, 2, 3, 4, etc.) par le deplacement d'une ligne vers le haut, puis une colonne vers la droite. Vous remarquerez immediatement que, pour placer le numero 2, vous passerez au-dessus de la rangee du haut, hors du carre magique. Ce n'est pas grave meme si vous travaillez toujours dans cette, droite une maniere, il y a trois exceptions qui ont egalement des motifs, previsible regles:
- Si le mouvement prend de vous une “boîte” au-dessus du carre magique de la rangee du haut, de rester dans la zone de la colonne, mais de placer le numero de la ligne du bas de la colonne.
- Si le mouvement prend de vous une “boîte” a droite du carre magique de la colonne de droite, rester dans la zone de ligne, mais le nombre le plus a gauche de la colonne de cette ligne.
- Si le mouvement prend de vous une case est deja occupee, revenir a la derniere case qui a ete rempli, et le lieu du prochain numero directement au-dessous.
@@_
@@
Methode 2
Resolution d'un Seul Meme Carre Magique


1
@@_
@@Comprendre ce qu'est un seul meme place. Tout le monde sait qu'un nombre est divisible par 2, mais dans les carres magiques, il existe differentes methodes pour resoudre individuellement et doublement meme places.
- Une seule encore place a un certain nombre de cases par cote qui est divisible par 2, mais pas 4.[2]
- Le plus petit possible individuellement, meme carre magique est 6x6, depuis 2x2 carres magiques ne peuvent pas etre faites.


2
@@_
@@Calculer la magie de la constante. Utilisez la meme methode que vous le feriez avec bizarre carres magiques: la magie de la constante = [n * (n^2 1)] / 2, ou n = le nombre de cases de chaque cote. Ainsi, dans l'exemple d'un carre 6x6:
- somme = [6 * (62 1)] / 2
- somme = [6 * (36 1)] / 2
- somme = (6 * 37) / 2
- somme = 222 / 2
- La magie constante pour un 6x6 carre est 222/2, ou 111.
- Toutes les lignes, colonnes et diagonales faut ajouter a ce nombre.


3
@@_
@@Diviser le carre magique en quatre quadrants de taille egale. Etiquette eux Une (en haut a gauche), C (en haut a droite), D (en bas a gauche) et B (en bas a droite). Pour determiner la taille de chaque carre doit etre, il suffit de diviser le nombre de cases dans chaque ligne ou colonne de moitie.
- Donc, pour un 6x6 carre, chaque quadrant de 3x3 cases.


4
@@_
@@Attribuer a chaque quadrant d'un numero de plage. Quadrant A devient pour le trimestre de nombres Quadrant B du deuxieme trimestre Quadrant C le troisieme trimestre, et le Quadrant D le dernier quart du nombre total de gamme pour les 6x6 carre magique.
- Dans l'exemple d'un carre 6x6, le Quadrant serait resolu avec les nombres de 1 a 9 Quadrant B avec 10-18 Quadrant C avec 19-27 et le Quadrant D avec 28-36.


5
@@_
@@Resoudre chaque quadrant a l'aide de la methodologie pour l'impair, les carres magiques. Quadrant A sera simple a remplir, car il commence avec le numero 1, comme les carres magiques d'habitude. Les Quadrants B-D, cependant, sera de commencer avec des numeros etranges — 10, 19 et 28, respectivement, dans notre exemple.
- Traiter le premier nombre de chaque quadrant, comme si elle est le numero un. Le placer dans la boîte de centre sur la ligne superieure de chaque quadrant.
- Traiter chaque quadrant comme son propre carre magique. Meme si une case est disponible a cote d'un quadrant, de l'ignorer et passer a la “exception” a la regle qui s'adapte a votre situation.


6
@@_
@@Creer des reflets A et D.[3] Si vous avez essaye d'ajouter vos colonnes, les lignes et les diagonales de droite maintenant, vous remarqueriez qu'ils n'ont pas encore ajouter a votre magie constante. Vous avez a echanger quelques cases entre le haut a gauche et en bas a gauche quadrants pour terminer votre carre magique. Nous allons appeler ces echange des zones de Surbrillance et de mettre en Evidence Un D.
- a l'Aide d'un crayon, marquer toutes les cases de la rangee du haut, jusqu'a ce que vous lisez la mediane de la position de la zone de Quadrant A. Donc, dans un carre 6x6, vous ne cochez la Case 1 (ce qui aurait le nombre de 8), mais dans un carre de 10x10, vous marquez les Cases 1 et 2 (qui aurait les numeros 17 et 24, respectivement).
- Marquer un carre en utilisant les cases vous juste marque que la ligne du haut. Si vous avez seulement une case, votre place est juste que d'un seul boîtier. Nous allons appeler ce domaine Soulignent Un-1.
- Donc, dans un 10x10 carre magique, mettez en Surbrillance Un-1 serait compose de Cases 1 et 2 dans les Lignes 1 et 2, de la creation d'un carre 2x2 en haut a gauche du quadrant.
- Dans la ligne directement en dessous de mettre en Evidence Un-1, ignorez le nombre dans la premiere colonne, puis cochez autant de cases de l'echelle que vous avez marque en Evidence Un-1. Nous allons appeler cette ligne du milieu en Evidence Un-2.
- mettre en Evidence Un-3 est une boîte identique a A-1, mais place dans le coin en bas a gauche du quadrant.
- mettre en Evidence Un-1, A-2 et A-3, ensemble, constituent en Evidence A.
- Repetez ce processus dans le Quadrant D, la creation d'un identique zone en surbrillance appele Highlight D.


7
@@_
@@Swap met en lumiere Un et D. C'est un un-a-un swap, il suffit de soulever et de remplacer les cases entre les Quadrants A et Quadrant D sans changer leur ordre. Une fois que vous avez fait cela, toutes les lignes, colonnes et diagonales dans votre carre magique devrait ajouter a la magie de la constante que vous avez calcule.@@_
@@
Methode 3
Resolution d'un Doublement Meme le Carre Magique


1
@@_
@@Comprendre ce qu'est un doublement meme place. Une seule encore place a un certain nombre de cases par cote qui est divisible par 2. Un doublement meme place a un certain nombre de cases de chaque cote divisible par double — 4.[4]
- Le plus petit doublement la meme boîte qui peut etre faite est un 4x4 place.


2
@@_
@@Calculer la magie de la constante. Utilisez la meme methode que vous le feriez avec un chiffre impair, soit separement-meme les carres magiques: la magie de la constante = [n * (n^2 1)] / 2, ou n = le nombre de cases de chaque cote. Ainsi, dans l'exemple d'un 4x4 place:
- somme = [4 * (4^2 1)] / 2
- somme = [4 * (16 1)] / 2
- somme = (4 * 17) / 2
- somme = 68 / 2
- La magie constante pour un 4x4 carre est 68/2, ou 34.
- Toutes les lignes, colonnes et diagonales faut ajouter a ce nombre.


3
@@_
@@Creer des reflets A-D. Dans chaque coin du carre magique, de la marque une mini-carre avec des cotes de longueur n/4, ou n = la longueur d'un cote de l'ensemble du carre magique.[5] Label met en lumiere Une, B, C et D dans le sens antihoraire.
- Dans un 4x4 place, il vous suffit de marquer les quatre coins des boîtes.
- Dans un 8x8 carre, chaque Souligner serait une 2x2 zone dans les coins.
- Dans un carre 12x12, chaque Souligner serait une zone de 3x3 dans les coins, et ainsi de suite.


4
@@_
@@Creer la Centrale de point culminant. Coche toutes les cases dans le centre du carre magique dans une zone carree de taille n/2, ou n = la longueur d'un cote de l'ensemble du carre magique. La Centrale de mettre en Evidence devrait se chevauchent pas avec les faits Saillants de l'A-D, toucher chacun d'entre eux dans les coins.
- Dans un 4x4 carre, la Centrale de mettre en Evidence serait une 2x2 zone dans le centre.
- Dans un 8x8 carre, la Centrale de mettre en Evidence serait un 4x4 de la zone dans le centre, et ainsi de suite.


5
@@_
@@Remplir le carre magique, mais seulement dans les zones en Surbrillance. Commencer a remplir les numeros de votre carre magique de gauche a droite, mais seulement ecrire le nombre si la boîte de releve d'une Evidence. Donc, dans un 4x4 boîte, vous renseignez les zones suivantes:
- 1 en haut a gauche de la boîte et 4 dans le top-case de droite
- 6 et 7 dans le centre de boîtes dans la Ligne 2
- 10 et 11 dans le centre de boîtes a la Ligne 3
- 13 dans le coin inferieur gauche de la boîte et 16 dans le coin inferieur droit de la boîte.


6
@@_
@@Remplir le reste du carre magique par comptage a rebours. Le est essentiellement l'inverse de l'etape precedente. Recommencer avec la case en haut a gauche, mais cette fois, ignorer toutes les boîtes qui tombent dans la zone en Surbrillance, et remplissez la non-mise en evidence des boîtes par un comptage a rebours. Commencer avec le plus grand nombre dans votre gamme de nombre. Donc, dans un carre magique 4x4, vous remplissez les suivantes:
- 15 et 14 dans le centre de boîtes a la Ligne 1
- 12 dans le menu le plus a gauche et 9 a droite dans la Ligne 2
- 8 dans le menu le plus a gauche et 5 a droite de la boîte dans la Ligne 3
- 3 et 2 dans le centre de cases sur la Ligne 4
- A ce stade, tous vos colonnes, les lignes et les diagonales doivent jusqu'a votre magie constant que vous avez calcule.
Comment Résoudre un Carré Magique
By commentfaire
Les carrés magiques ont gagné en popularité avec l'avènement des mathématiques basés sur des jeux comme le Sudoku. Un carré magique est un arrangement de nombres dans un carré de telle manière que la somme de chaque ligne, colonne et diagonale est un nombre constant, le soi-disant "magique constante." Cet article va vous dire comment résoudre n'importe quel type de carré magique, si impaires, seul paire, ou une double paire.