Dans les statistiques, la fréquence absolue désigne le nombre de fois qu'une valeur particulière apparaît dans un ensemble de données. La fréquence cumulée est différente: c'est la somme (ou total) de toutes les fréquences jusqu'au point courant dans l'ensemble de données. Ne vous inquiétez pas si cela sonne comme le jargon, c'est plus facile lorsque vous suivez avec un stylo et du papier.
Mesures
@@_
@@
Partie 1
Base de la Fréquence Cumulée
1
@@_
@@Trier l'ensemble de données. Un 'ensemble de données' est juste le groupe de numéros que vous étudiez. Trier ces valeurs dans l'ordre, du plus petit au plus grand.
- Exemple: Votre ensemble de données indique le nombre de livres que chaque élève a lu dans le dernier mois. Après le tri, c'est l'ensemble de données: 3, 3, 5, 6, 6, 6, 8.


2
@@_
@@Compter la fréquence absolue de chaque valeur. La fréquence d'une valeur est le nombre de fois que la valeur s'affiche. (Vous pouvez appeler cela la 'fréquence absolue' quand vous en avez besoin pour éviter la confusion avec la fréquence cumulée.) La façon la plus simple de garder une trace de ce est de commencer un graphique. Écrire la 'Valeur' (ou une description de ce que les mesures de valeur) au début de la première colonne. Écrire 'Fréquence' en haut de la deuxième colonne. Remplissez le tableau pour chaque valeur.
- par Exemple: Écrire 'Nombre de Livres' en haut de la première colonne. Écrire 'Fréquence' en haut de la deuxième colonne.
- Dans la deuxième ligne, écrire à la première valeur sous le Nombre de Livres: 3.
- Compter le nombre de 3 dans votre jeu de données. Puisqu'il y a deux 3s, écrire 2 en dessous de la Fréquence sur la même ligne.
- Répétez l'opération pour chaque valeur jusqu'à ce que vous avez la pleine graphique:
- 3 | F = 2
- 5 | F = 1
- 6 | F = 3
- 8 | F = 1


3
@@_
@@Trouver la fréquence cumulée de la première valeur. La fréquence cumulée des réponses à la question 'combien de fois cette valeur ou une valeur plus faible?' Toujours commencer avec la valeur la plus basse dans votre jeu de données. Depuis il n'y a pas de petites valeurs, la réponse est la même que celle de la valeur absolue de la fréquence.
- Exemple: Notre valeur la plus basse est de 3. Le nombre d'élèves qui ont lu 3 livres 2. Personne ne lisent moins que ça, alors que la fréquence cumulée est de 3. L'ajouter à la première ligne de votre tableau:


4
@@_
@@Trouver la prochaine valeur de la fréquence cumulée. Passer à la valeur suivante sur votre graphique. Nous venons de trouver combien de fois les plus faibles valeurs ont montré jusqu'à. Pour trouver la fréquence cumulée de cette valeur, nous avons juste besoin de les ajouter à sa fréquence absolue de la course totale. En d'autres termes, prendre la dernière fréquence cumulée que vous avez trouvé, puis ajouter cette valeur absolue de la fréquence.
- Exemple:
- 3 | F = 2 | CF = 2
- 5 | F = 1 | CF = 2 1 = 3


5
@@_
@@Répétez l'opération pour le reste des valeurs. Continuer à aller de plus en plus grande des valeurs. À chaque fois, ajouter la dernière fréquence cumulée à la valeur absolue de la fréquence.
- Exemple:
- 3 | F = 2 | CF = 2
- 5 | F = 1 | CF = 2 1 = 3
- 6 | F = 3 | CF = 3 3 = 6
- 8 | F = 1 | CF = 6 1 = 7


6
@@_
@@Vérifier votre travail. Une fois que vous avez terminé, vous avez ajoutées, ensemble, le nombre de fois que chaque variable est apparu. Le final de la fréquence cumulée doit être égal au nombre total de points de données dans votre ensemble. Il y a deux façons de vérifier ceci:
- Ajouter toutes les fréquences ensemble: 2 1 3 1 = 7, ce qui est notre finale de la fréquence cumulée.
- Compter le nombre de points de données. Notre liste a été 3, 3, 5, 6, 6, 6, 8. Il y a 7 éléments, ce qui est notre finale de la fréquence cumulée.
@@_
@@
Partie 2
Utilisation Avancée


1
@@_
@@Comprendre discrètes et continues de données. Discret données dans les unités que vous pouvez compter, où il est impossible de trouver une partie d'une unité. Les données en continu décrit quelque chose d'indéfinissable, avec les mesures que pourrait se situer n'importe où entre ce que les unités que vous choisissez. Voici quelques exemples:
- Nombre de chiens: Discret. Il n'y a pas une telle chose comme un demi-chien.
- Profondeur de la neige: Continue. La neige s'accumule graduellement, non pas en une seule unité à la fois. Si vous avez essayé de le mesurer en pouces, vous pouvez trouver un tas de neige qui était de 5,6 pouces de profondeur.


2
@@_
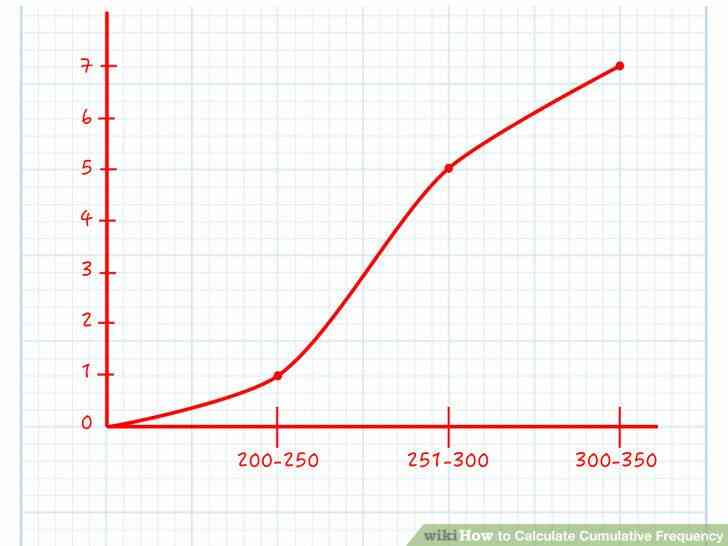
@@Groupe de données en continu par gamme. Continue ensembles de données ont souvent un grand nombre de variables uniques. Si vous avez essayé d'utiliser la méthode ci-dessus, le tableau serait très long, et difficile à comprendre. Au lieu de cela, faire de chaque ligne de votre tableau une plage de valeurs. Il est important de faire de chaque gamme de la même taille (comme de 0 à 10, 11 à 20, 21 à 30, etc.), peu importe le nombre de valeurs dans chaque gamme. Voici un exemple d'un processus continu série de données transformé en un tableau:
- jeu de Données: 233, 259, 277, 278, 289, 301, 303
- Graphique (première valeur de la colonne, deuxième colonne de la fréquence, de la troisième colonne de la fréquence cumulée):
- 200-250 | 1 | 1
- 251-300 | 4 | 1 4 = 5
- 301-350 | 2 | 5 2 = 7

3
@@_
@@Faire une ligne graphique. Une fois que vous avez calculé la fréquence cumulée, sortir un papier millimétré. Tracer une ligne graphique avec l'axe des x égale aux valeurs de votre ensemble de données, et l'axe des y égale à la fréquence cumulée. Cela rendra la prochaine calculs beaucoup plus facile.
- Par exemple, si votre jeu de données va de 1 à 8, tracez un axe x avec huit unités marquées sur elle. À chaque valeur sur l'axe des x, tracer un point à la valeur de y est égale à la fréquence cumulée à cette valeur. Connectez chaque paire de points adjacents avec une ligne.
- Si il n'y a pas de points de données à une valeur particulière, la fréquence absolue est de 0. L'ajout de 0 jusqu'à la dernière fréquence cumulée ne change pas sa valeur, afin de tracer un point à la même valeur de y comme la dernière valeur.
- en Raison de la fréquence cumulée augmente toujours avec les valeurs, votre ligne graphique doit toujours rester stable ou d'aller comme il se déplace vers la droite. Si la ligne passe à n'importe quel moment, vous pourriez être à la recherche à la fréquence absolue par erreur.

4
@@_
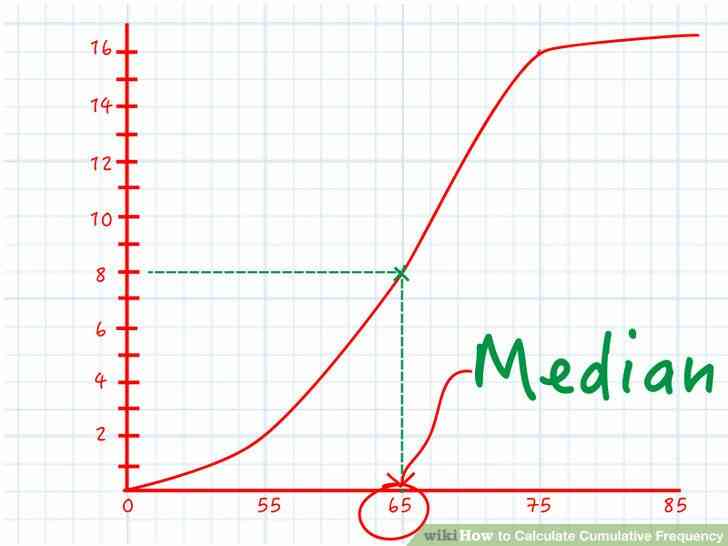
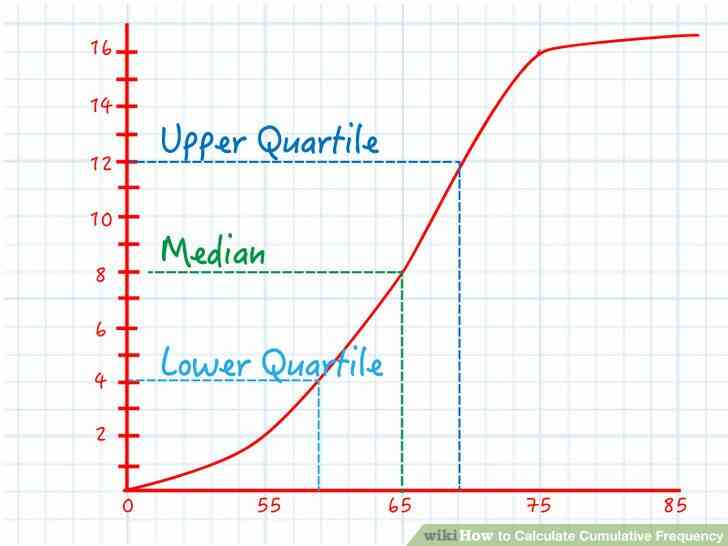
@@Trouver la médiane de la ligne graphique. La médiane est la valeur exactement au milieu de l'ensemble de données. La moitié des valeurs sont au-dessus de la médiane et l'autre moitié en dessous. Voici comment trouver la médiane sur votre ligne graphique:
- Regarder le dernier point sur l'extrême droite de votre graphique. Sa y est la valeur totale cumulée fréquence, qui est le nombre de points dans l'ensemble de données. Disons que cette valeur est 16
- Multiplier cette valeur par ½ et de le trouver sur l'axe des ordonnées. Dans notre exemple, la moitié de 16 à 8. Trouver 8 sur l'axe des y.
- Trouver le point sur la ligne graphique à cette valeur de y la. Déplacez votre doigt à partir de la 8 sur l'axe des y sur le graphique. Arrêter lorsque votre doigt touche la ligne de votre graphique. C'est le point où exactement à la moitié de vos points de données ont été recensées.
- Trouver l'axe des x à ce point. Déplacez votre doigt vers le bas à voir avec l'axe des x de la valeur. Cette valeur est la médiane de votre ensemble de données. Par exemple, si cette valeur est de 65 ans, alors la moitié de votre ensemble de données est en dessous de 65 ans, et la moitié est au-dessus de 65 ans.

5
@@_
@@Trouver les quartiles de la ligne graphique. Les Quartiles de diviser les données en quatre sections. Ce processus est très similaire à la recherche de la médiane. La seule différence est la façon dont vous trouverez les valeurs de y:
- Pour trouver le quartile inférieur de la valeur de l'axe y, prendre le maximum de la fréquence cumulée et de la multiplier par¼. La correspondante de la valeur x indique la valeur avec exactement ¼ des données ci-dessous.
- Pour trouver le quartile supérieur de la valeur de l'axe y, il faut multiplier le maximum de la fréquence cumulée de¾. La correspondante de la valeur x indique la valeur avec exactement les ¾ des données ci-dessous et ¼ au-dessus d'elle.
Comment Calculer la Frequence Cumulee
Dans les statistiques, la frequence absolue designe le nombre de fois qu'une valeur particuliere apparaît dans un ensemble de donnees. La frequence cumulee est differente: c'est la somme (ou total) de toutes les frequences jusqu'au point courant dans l'ensemble de donnees. Ne vous inquietez pas si cela sonne comme le jargon, c'est plus facile lorsque vous suivez avec un stylo et du papier.
Mesures
@@_
@@
Partie 1
Base de la Frequence Cumulee
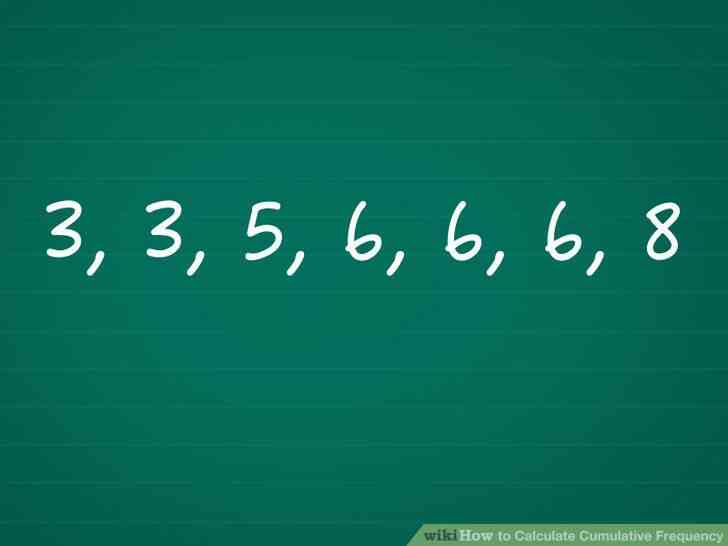
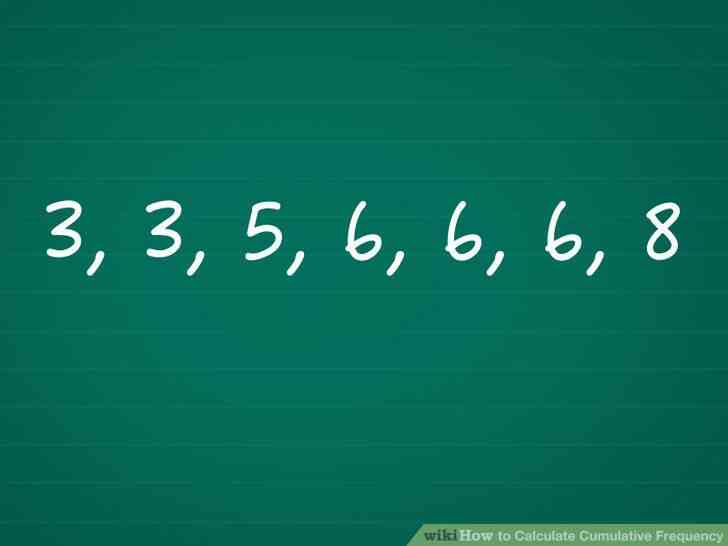
1
@@_
@@Trier l'ensemble de donnees. Un 'ensemble de donnees' est juste le groupe de numeros que vous etudiez. Trier ces valeurs dans l'ordre, du plus petit au plus grand.
- Exemple: Votre ensemble de donnees indique le nombre de livres que chaque eleve a lu dans le dernier mois. Apres le tri, c'est l'ensemble de donnees: 3, 3, 5, 6, 6, 6, 8.


2
@@_
@@Compter la frequence absolue de chaque valeur. La frequence d'une valeur est le nombre de fois que la valeur s'affiche. (Vous pouvez appeler cela la 'frequence absolue' quand vous en avez besoin pour eviter la confusion avec la frequence cumulee.) La façon la plus simple de garder une trace de ce est de commencer un graphique. Ecrire la 'Valeur' (ou une description de ce que les mesures de valeur) au debut de la premiere colonne. Ecrire 'Frequence' en haut de la deuxieme colonne. Remplissez le tableau pour chaque valeur.
- par Exemple: Ecrire 'Nombre de Livres' en haut de la premiere colonne. Ecrire 'Frequence' en haut de la deuxieme colonne.
- Dans la deuxieme ligne, ecrire a la premiere valeur sous le Nombre de Livres: 3.
- Compter le nombre de 3 dans votre jeu de donnees. Puisqu'il y a deux 3s, ecrire 2 en dessous de la Frequence sur la meme ligne.
- Repetez l'operation pour chaque valeur jusqu'a ce que vous avez la pleine graphique:
- 3 | F = 2
- 5 | F = 1
- 6 | F = 3
- 8 | F = 1


3
@@_
@@Trouver la frequence cumulee de la premiere valeur. La frequence cumulee des reponses a la question 'combien de fois cette valeur ou une valeur plus faible?' Toujours commencer avec la valeur la plus basse dans votre jeu de donnees. Depuis il n'y a pas de petites valeurs, la reponse est la meme que celle de la valeur absolue de la frequence.
- Exemple: Notre valeur la plus basse est de 3. Le nombre d'eleves qui ont lu 3 livres 2. Personne ne lisent moins que ça, alors que la frequence cumulee est de 3. L'ajouter a la premiere ligne de votre tableau:


4
@@_
@@Trouver la prochaine valeur de la frequence cumulee. Passer a la valeur suivante sur votre graphique. Nous venons de trouver combien de fois les plus faibles valeurs ont montre jusqu'a. Pour trouver la frequence cumulee de cette valeur, nous avons juste besoin de les ajouter a sa frequence absolue de la course totale. En d'autres termes, prendre la derniere frequence cumulee que vous avez trouve, puis ajouter cette valeur absolue de la frequence.
- Exemple:
- 3 | F = 2 | CF = 2
- 5 | F = 1 | CF = 2 1 = 3


5
@@_
@@Repetez l'operation pour le reste des valeurs. Continuer a aller de plus en plus grande des valeurs. A chaque fois, ajouter la derniere frequence cumulee a la valeur absolue de la frequence.
- Exemple:
- 3 | F = 2 | CF = 2
- 5 | F = 1 | CF = 2 1 = 3
- 6 | F = 3 | CF = 3 3 = 6
- 8 | F = 1 | CF = 6 1 = 7


6
@@_
@@Verifier votre travail. Une fois que vous avez termine, vous avez ajoutees, ensemble, le nombre de fois que chaque variable est apparu. Le final de la frequence cumulee doit etre egal au nombre total de points de donnees dans votre ensemble. Il y a deux façons de verifier ceci:
- Ajouter toutes les frequences ensemble: 2 1 3 1 = 7, ce qui est notre finale de la frequence cumulee.
- Compter le nombre de points de donnees. Notre liste a ete 3, 3, 5, 6, 6, 6, 8. Il y a 7 elements, ce qui est notre finale de la frequence cumulee.
@@_
@@
Partie 2
Utilisation Avancee


1
@@_
@@Comprendre discretes et continues de donnees. Discret donnees dans les unites que vous pouvez compter, ou il est impossible de trouver une partie d'une unite. Les donnees en continu decrit quelque chose d'indefinissable, avec les mesures que pourrait se situer n'importe ou entre ce que les unites que vous choisissez. Voici quelques exemples:
- Nombre de chiens: Discret. Il n'y a pas une telle chose comme un demi-chien.
- Profondeur de la neige: Continue. La neige s'accumule graduellement, non pas en une seule unite a la fois. Si vous avez essaye de le mesurer en pouces, vous pouvez trouver un tas de neige qui etait de 5,6 pouces de profondeur.


2
@@_
@@Groupe de donnees en continu par gamme. Continue ensembles de donnees ont souvent un grand nombre de variables uniques. Si vous avez essaye d'utiliser la methode ci-dessus, le tableau serait tres long, et difficile a comprendre. Au lieu de cela, faire de chaque ligne de votre tableau une plage de valeurs. Il est important de faire de chaque gamme de la meme taille (comme de 0 a 10, 11 a 20, 21 a 30, etc.), peu importe le nombre de valeurs dans chaque gamme. Voici un exemple d'un processus continu serie de donnees transforme en un tableau:
- jeu de Donnees: 233, 259, 277, 278, 289, 301, 303
- Graphique (premiere valeur de la colonne, deuxieme colonne de la frequence, de la troisieme colonne de la frequence cumulee):
- 200-250 | 1 | 1
- 251-300 | 4 | 1 4 = 5
- 301-350 | 2 | 5 2 = 7


3
@@_
@@Faire une ligne graphique. Une fois que vous avez calcule la frequence cumulee, sortir un papier millimetre. Tracer une ligne graphique avec l'axe des x egale aux valeurs de votre ensemble de donnees, et l'axe des y egale a la frequence cumulee. Cela rendra la prochaine calculs beaucoup plus facile.
- Par exemple, si votre jeu de donnees va de 1 a 8, tracez un axe x avec huit unites marquees sur elle. A chaque valeur sur l'axe des x, tracer un point a la valeur de y est egale a la frequence cumulee a cette valeur. Connectez chaque paire de points adjacents avec une ligne.
- Si il n'y a pas de points de donnees a une valeur particuliere, la frequence absolue est de 0. L'ajout de 0 jusqu'a la derniere frequence cumulee ne change pas sa valeur, afin de tracer un point a la meme valeur de y comme la derniere valeur.
- en Raison de la frequence cumulee augmente toujours avec les valeurs, votre ligne graphique doit toujours rester stable ou d'aller comme il se deplace vers la droite. Si la ligne passe a n'importe quel moment, vous pourriez etre a la recherche a la frequence absolue par erreur.


4
@@_
@@Trouver la mediane de la ligne graphique. La mediane est la valeur exactement au milieu de l'ensemble de donnees. La moitie des valeurs sont au-dessus de la mediane et l'autre moitie en dessous. Voici comment trouver la mediane sur votre ligne graphique:
- Regarder le dernier point sur l'extreme droite de votre graphique. Sa y est la valeur totale cumulee frequence, qui est le nombre de points dans l'ensemble de donnees. Disons que cette valeur est 16
- Multiplier cette valeur par ½ et de le trouver sur l'axe des ordonnees. Dans notre exemple, la moitie de 16 a 8. Trouver 8 sur l'axe des y.
- Trouver le point sur la ligne graphique a cette valeur de y la. Deplacez votre doigt a partir de la 8 sur l'axe des y sur le graphique. Arreter lorsque votre doigt touche la ligne de votre graphique. C'est le point ou exactement a la moitie de vos points de donnees ont ete recensees.
- Trouver l'axe des x a ce point. Deplacez votre doigt vers le bas a voir avec l'axe des x de la valeur. Cette valeur est la mediane de votre ensemble de donnees. Par exemple, si cette valeur est de 65 ans, alors la moitie de votre ensemble de donnees est en dessous de 65 ans, et la moitie est au-dessus de 65 ans.


5
@@_
@@Trouver les quartiles de la ligne graphique. Les Quartiles de diviser les donnees en quatre sections. Ce processus est tres similaire a la recherche de la mediane. La seule difference est la façon dont vous trouverez les valeurs de y:
- Pour trouver le quartile inferieur de la valeur de l'axe y, prendre le maximum de la frequence cumulee et de la multiplier par¼. La correspondante de la valeur x indique la valeur avec exactement ¼ des donnees ci-dessous.
- Pour trouver le quartile superieur de la valeur de l'axe y, il faut multiplier le maximum de la frequence cumulee de¾. La correspondante de la valeur x indique la valeur avec exactement les ¾ des donnees ci-dessous et ¼ au-dessus d'elle.
Comment Calculer la Fréquence Cumulée
By commentfaire
Dans les statistiques, la fréquence absolue désigne le nombre de fois qu'une valeur particulière apparaît dans un ensemble de données. La fréquence cumulée est différente: c'est la somme (ou total) de toutes les fréquences jusqu'au point courant dans l'ensemble de données. Ne vous inquiétez pas si cela sonne comme le jargon, c'est plus facile lorsque vous suivez avec un stylo et du papier.