Un vecteur est un objet géométrique qui a la direction et de l'ampleur. Il peut être représenté comme un segment de ligne avec un point initial (point de départ) à une extrémité et d'une flèche à l'autre extrémité, de telle sorte que la longueur du segment de ligne est la magnitude du vecteur et de la flèche indique la direction du vecteur. Vecteur de normalisation est un exercice commun en mathématiques et il a aussi des applications pratiques en infographie.
Mesures
@@_
@@
Méthode 1
Définir les Termes

1
@@_
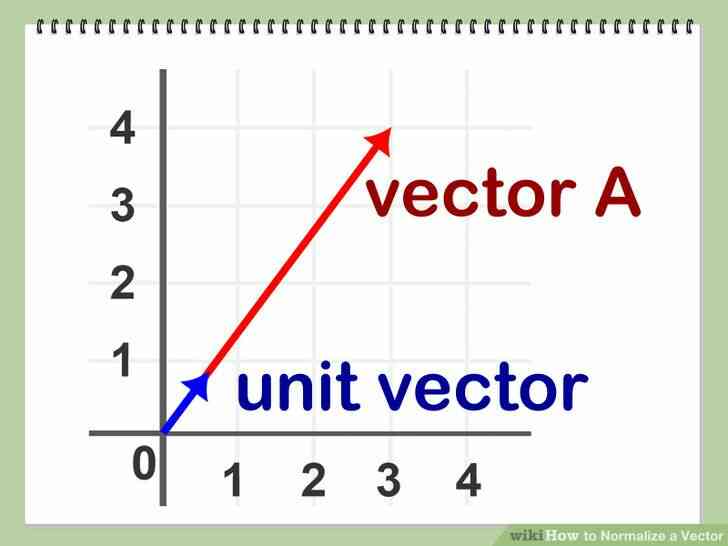
@@Définir un vecteur unitaire. Le vecteur unitaire d'un vecteur est le vecteur avec le même point de départ et la direction, comme Un, mais avec une longueur de 1 unité. Il peut être mathématiquement prouvé qu'il existe un et un seul vecteur unitaire pour chaque vecteur A.

2
@@_
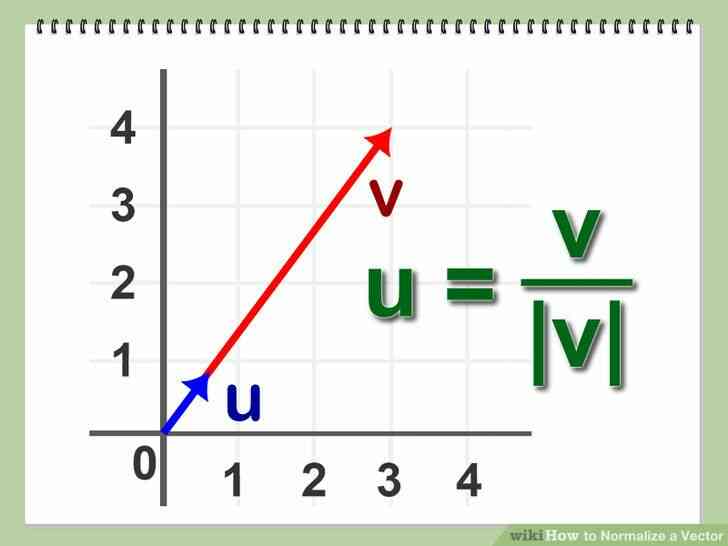
@@Définir la Normalisation d'un vecteur. C'est le processus d'identification de l'unité de vecteur pour un vecteur donné A.

3
@@_
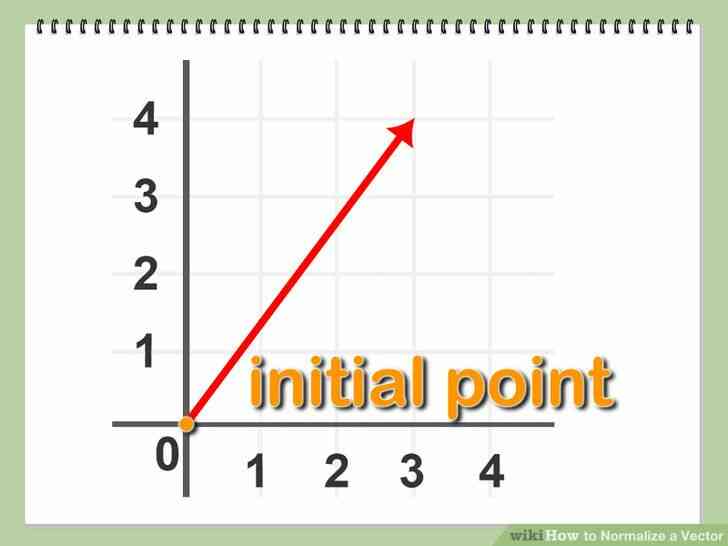
@@Définir un vecteur lié. Un vecteur lié dans Cartésien l'espace a son point de départ, à l'origine du système de coordonnées, exprimée en (0,0) en deux dimensions. Cela vous permet d'identifier un vecteur uniquement en termes de son point terminal.

4
@@_
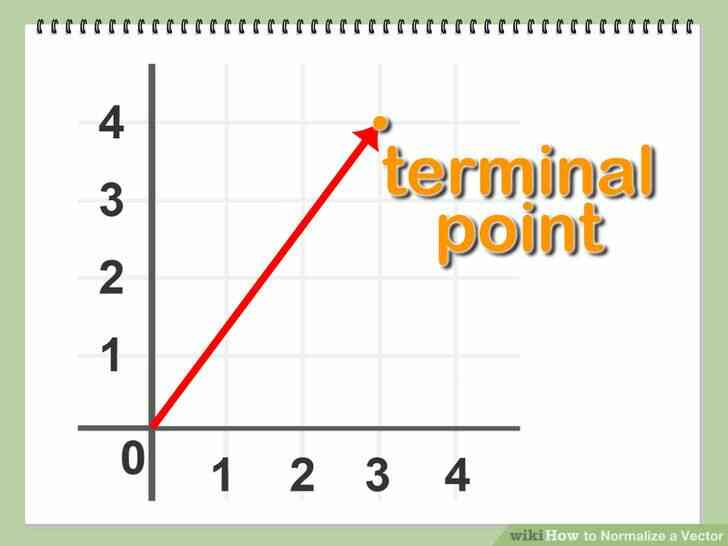
@@Décrire vecteur de notation. Par de nous limiter à lié vecteurs A = (x, y), où la paire de coordonnées (x,y) indique l'emplacement de la borne de vecteur A.@@_
@@
Méthode 2
Analyser l'Objectif

1
@@_
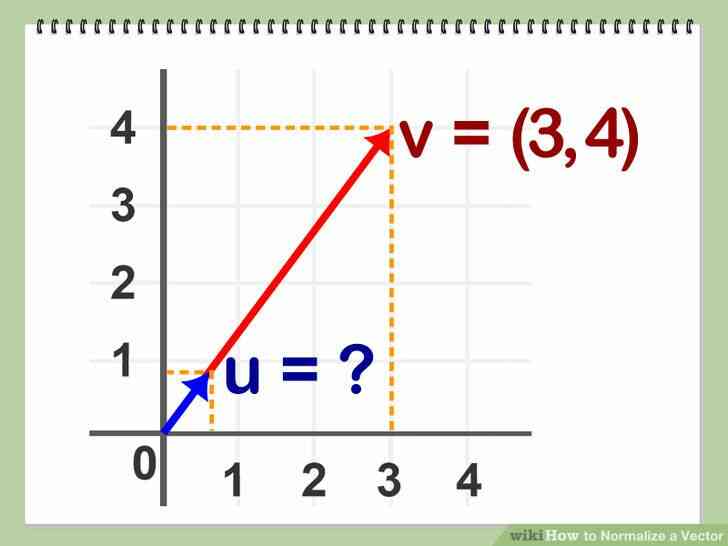
@@Établir les valeurs connues. À partir de la définition de l'unité de vecteur, nous savons que le point initial et la direction du vecteur unitaire est le même que le vecteur A. de Plus, nous savons que la longueur du vecteur unitaire est de 1.


2
@@_
@@Déterminer la valeur inconnue. La seule variable que nous besoin de calculer est le point terminal de l'unité de vecteur.@@_
@@
Méthode 3
dégager une Solution pour le Vecteur Unitaire
- Trouver le point terminal de l'unité de vecteur de vecteur A = (x, y). À partir de la proportionnalité de semblable, triangles, vous savez que tout vecteur qui a la même direction que le vecteur d'Une aura un terminal point (x/c, y/c) pour certains c. En outre, vous savez la longueur du vecteur unitaire est de 1. Par conséquent, par la Pythagore Théorème, [x^2/c^2 y^2/c^2]^(1/2) = 1 -> [(x^2 y^2)/c^2]^(1/2) -> (x^2 y^2)^(1/2)/c = 1 -> c = (x^2 y^2)^(1/2). Par conséquent, le vecteur unitaire u pour le vecteur A = (x, y) est donnée comme u = (x/(x^2 y^2)^(1/2), y/(x^2 y^2)^(1/2))


@@_
@@
Méthode 4
Normaliser un Vecteur dans l'Espace à 2 Dimensions
- Laisser Un vecteur un vecteur avec son point de départ, à l'origine et le terminal de point (2,3), tel que A = (2,3). Calculer le vecteur unitaire u = (x/(x^2 y^2)^(1/2), y/(x^2 y^2)^(1/2)) = (2/(2^2 3^2)^(1/2), 3/(2^2 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Par conséquent, A = (2,3) normalise à u = (2/(13^(1/2)), 3/(13^(1/2))).


@@_
@@
Méthode 5
Normaliser un Vecteur dans l'Espace à n Dimensions
- Généraliser l'équation du vecteur de normalisation dans l'espace de dimension. Un vecteur (A, b, c, ...), u = (a/z, b/z, c/z, ...) où z = (a^2 b^2 c^2 ...)^(1/2).
Comment Normaliser un Vecteur
Un vecteur est un objet geometrique qui a la direction et de l'ampleur. Il peut etre represente comme un segment de ligne avec un point initial (point de depart) a une extremite et d'une fleche a l'autre extremite, de telle sorte que la longueur du segment de ligne est la magnitude du vecteur et de la fleche indique la direction du vecteur. Vecteur de normalisation est un exercice commun en mathematiques et il a aussi des applications pratiques en infographie.
Mesures
@@_
@@
Methode 1
Definir les Termes


1
@@_
@@Definir un vecteur unitaire. Le vecteur unitaire d'un vecteur est le vecteur avec le meme point de depart et la direction, comme Un, mais avec une longueur de 1 unite. Il peut etre mathematiquement prouve qu'il existe un et un seul vecteur unitaire pour chaque vecteur A.


2
@@_
@@Definir la Normalisation d'un vecteur. C'est le processus d'identification de l'unite de vecteur pour un vecteur donne A.


3
@@_
@@Definir un vecteur lie. Un vecteur lie dans Cartesien l'espace a son point de depart, a l'origine du systeme de coordonnees, exprimee en (0,0) en deux dimensions. Cela vous permet d'identifier un vecteur uniquement en termes de son point terminal.


4
@@_
@@Decrire vecteur de notation. Par de nous limiter a lie vecteurs A = (x, y), ou la paire de coordonnees (x,y) indique l'emplacement de la borne de vecteur A.@@_
@@
Methode 2
Analyser l'Objectif


1
@@_
@@Etablir les valeurs connues. A partir de la definition de l'unite de vecteur, nous savons que le point initial et la direction du vecteur unitaire est le meme que le vecteur A. de Plus, nous savons que la longueur du vecteur unitaire est de 1.


2
@@_
@@Determiner la valeur inconnue. La seule variable que nous besoin de calculer est le point terminal de l'unite de vecteur.@@_
@@
Methode 3
degager une Solution pour le Vecteur Unitaire
- Trouver le point terminal de l'unite de vecteur de vecteur A = (x, y). A partir de la proportionnalite de semblable, triangles, vous savez que tout vecteur qui a la meme direction que le vecteur d'Une aura un terminal point (x/c, y/c) pour certains c. En outre, vous savez la longueur du vecteur unitaire est de 1. Par consequent, par la Pythagore Theoreme, [x^2/c^2 y^2/c^2]^(1/2) = 1 -> [(x^2 y^2)/c^2]^(1/2) -> (x^2 y^2)^(1/2)/c = 1 -> c = (x^2 y^2)^(1/2). Par consequent, le vecteur unitaire u pour le vecteur A = (x, y) est donnee comme u = (x/(x^2 y^2)^(1/2), y/(x^2 y^2)^(1/2))


@@_
@@
Methode 4
Normaliser un Vecteur dans l'Espace a 2 Dimensions
- Laisser Un vecteur un vecteur avec son point de depart, a l'origine et le terminal de point (2,3), tel que A = (2,3). Calculer le vecteur unitaire u = (x/(x^2 y^2)^(1/2), y/(x^2 y^2)^(1/2)) = (2/(2^2 3^2)^(1/2), 3/(2^2 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Par consequent, A = (2,3) normalise a u = (2/(13^(1/2)), 3/(13^(1/2))).


@@_
@@
Methode 5
Normaliser un Vecteur dans l'Espace a n Dimensions
- Generaliser l'equation du vecteur de normalisation dans l'espace de dimension. Un vecteur (A, b, c, ...), u = (a/z, b/z, c/z, ...) ou z = (a^2 b^2 c^2 ...)^(1/2).
Comment Normaliser un Vecteur
By commentfaire
Un vecteur est un objet géométrique qui a la direction et de l'ampleur. Il peut être représenté comme un segment de ligne avec un point initial (point de départ) à une extrémité et d'une flèche à l'autre extrémité, de telle sorte que la longueur du segment de ligne est la magnitude du vecteur et de la flèche indique la direction du vecteur. Vecteur de normalisation est un exercice commun en mathématiques et il a aussi des applications pratiques en infographie.