Distance, souvent assignée à la variable d, est une mesure de l'espace, contenue par une ligne droite entre deux points. La Distance peut se référer à l'espace entre les deux points stationnaires (par exemple, la taille d'une personne est la distance entre le dessous de ses pieds vers le haut de sa tête) ou peut se référer à l'espace entre la position actuelle d'un objet en mouvement et de son emplacement de départ. Plus la distance les problèmes peuvent être résolus avec les équations d = savg × t où d est la distance, savg est la vitesse moyenne, et t est le temps, ou à l'aide d = √((x2 - x1)2 (y2 - y1)2), où (x1, y1) et (x2, y2) sont les coordonnées x et y de deux points.
Mesures
@@_
@@
Méthode 1
Trouver la Distance avec la Vitesse Moyenne et le Temps


1
@@_
@@Trouver les valeurs de vitesse moyenne et le temps. Lorsque vous essayez de trouver la distance d'un objet en mouvement a parcouru, deux informations sont essentielles pour faire ce calcul: sa vitesse (ou la vitesse de grandeur) et le temps qu'il a été en mouvement. Avec cette information, il est possible de trouver la distance à laquelle l'objet a voyagé à l'aide de la formule d = savg × t.
- Pour mieux comprendre le processus de l'aide de la formule de la distance, nous allons résoudre un exemple de problème dans cette section. Disons que nous sommes dévaler la route à 120 miles par heure (environ 193 km par heure) et nous voulons savoir où nous allons nous rendre dans une demi-heure. À l'aide de 120 km / h comme notre valeur pour la vitesse moyenne et 0.5 heures que la valeur de notre temps, nous allons résoudre ce problème dans la prochaine étape.


2
@@_
@@Multiplier la vitesse moyenne par heure. Une fois que vous connaissez la moyenne de la vitesse d'un objet en mouvement et le temps du voyage, trouver la distance qu'il a parcourue est relativement simple. Il suffit de multiplier ces deux quantités pour trouver votre réponse.
- Notez, cependant, que si les unités de temps utilisées dans votre moyenne de la valeur de la vitesse sont différentes de celles utilisées dans votre valeur de temps, vous aurez besoin de convertir un ou l'autre de sorte qu'ils sont compatibles. Par exemple, si nous avons une vitesse moyenne de la valeur qui est mesurée en km par heure et une valeur de temps est mesuré en minutes, vous devez diviser la valeur de temps de 60 à convertir en heures.
- nous allons résoudre notre exemple de problème. 120 km/h × 0,5 heure = 60 miles. Notez que les unités de la valeur de temps (heures) annuler avec les unités dans le dénominateur de la vitesse moyenne (en heures) pour ne laisser que les unités de distance (miles).
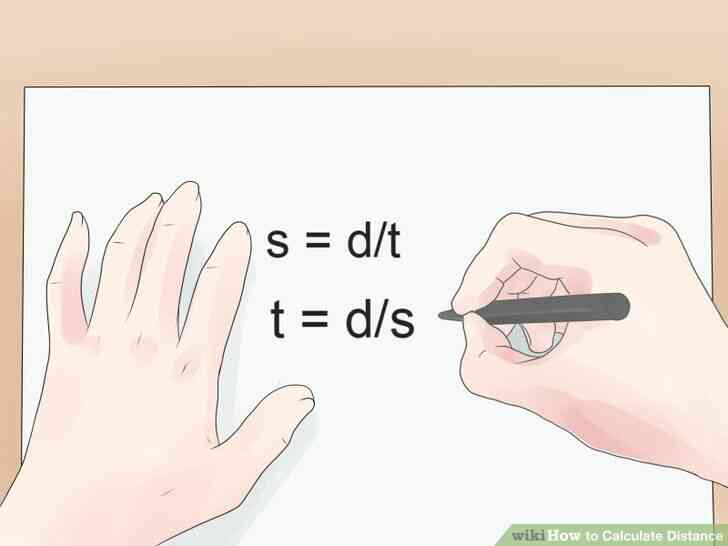
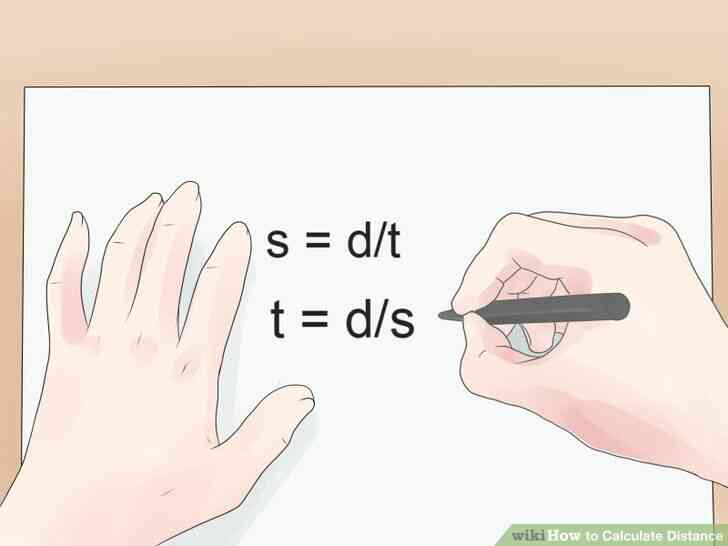
3
@@_
@@Manipuler l'équation à résoudre pour les autres variables. La simplicité de la base de la distance de l'équation (d = savg × t) le rend très facile à utiliser l'équation pour trouver les valeurs des variables en plus de la distance. Simplement pour isoler la variable que vous voulez résoudre selon les règles de base de la algèbre, puis insérez les valeurs de votre deux autres variables pour trouver la valeur de la troisième. En d'autres termes, pour trouver l'objet de votre vitesse moyenne, l'utilisation de l'équation savg = d/t et à trouver à trouver le temps un objet a voyagé, l'utilisation de l'équation t = d/savg.
- Par exemple, disons que nous savons qu'une voiture a conduit 60 km en 50 minutes, mais nous n'avons pas une valeur pour la vitesse moyenne lors d'un voyage. Dans ce cas, on peut isoler le savg variable dans la base de la distance de l'équation pour obtenir savg = d/t, alors il suffit de diviser 60 km / 50 minutes pour avoir une réponse de 1,2 miles/minute.
- a Noter que dans notre exemple, notre réponse pour la vitesse a une rare unités (km/minute). Pour obtenir votre réponse dans la forme la plus commune de miles/heure, de le multiplier par 60 minutes/heure pour atteindre 72 km/heure.


4
@@_
@@Remarque que le 'savg' variable dans la formule de la distance se réfère à vitesse moyenne. Il est important de comprendre que la formule de la distance offre une vue simplifiée du mouvement d'un objet. La formule de la distance suppose que l'objet en mouvement a une vitesse constante — en d'autres termes, on suppose que l'objet en mouvement se déplace à une unique, immuable taux de vitesse. Pour les mathématiques abstraites, des problèmes, tels que ceux que vous pouvez rencontrer dans un cadre académique, c'est parfois encore possible de modéliser un objet en mouvement à l'aide de cette hypothèse. Dans la vraie vie, cependant, ce modèle n'est souvent pas refléter avec précision le mouvement des objets en mouvement, ce qui peut, en réalité, accélérer, ralentir, arrêter et inverser le cours du temps.
- Par exemple, dans l'exemple ci-dessus, nous avons conclu que le voyage de 60 km en 50 minutes, nous aurions besoin de voyager à 72 km/heure. Cependant, cela n'est vrai que si le voyage à une vitesse pour la totalité du voyage. Par exemple, en voyageant à 80 km/h pour la moitié du voyage et de 64 km/heure pour l'autre moitié, on va encore en voyage de 60 km en 50 minutes — 72 milles/heure = 60 km/50 min. = ?????
- Calcul de solutions à base d' l'utilisation d'instruments dérivés sont souvent un meilleur choix que la formule de la distance pour la définition d'un objet de la vitesse dans les situations du monde réel parce que les changements de vitesse sont susceptibles.
@@_
@@
Méthode 2
Trouver la Distance entre Deux Points
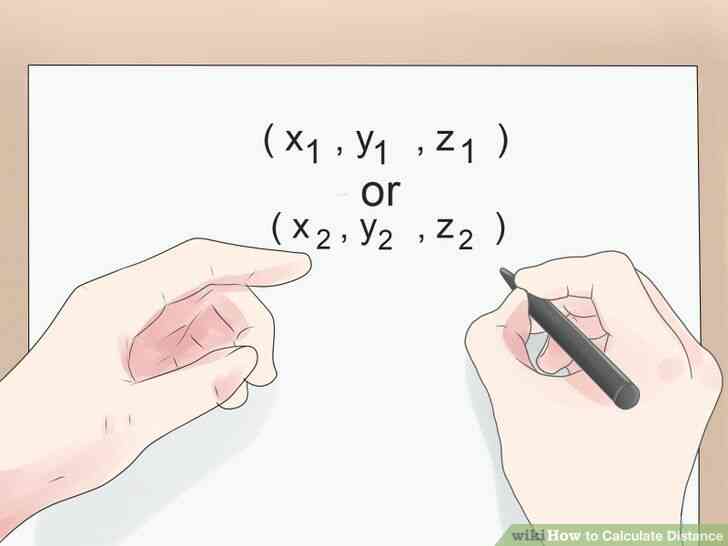
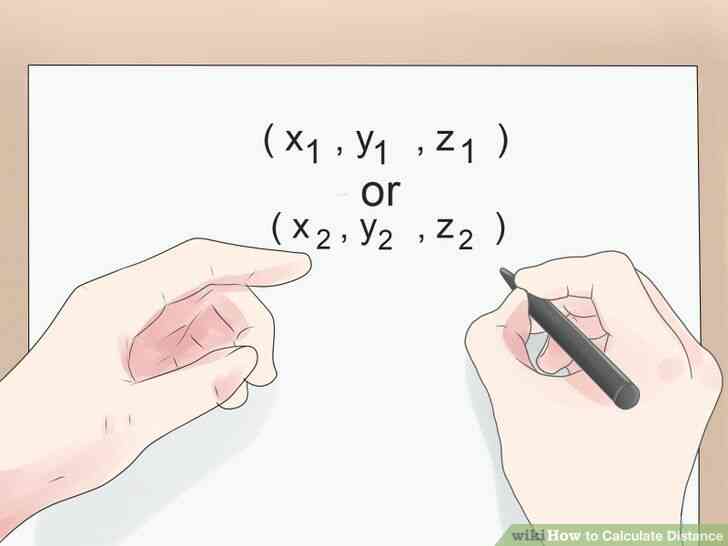
1
@@_
@@Trouver deux points de coordonnées spatiales. Et si, plutôt que de trouver la distance d'un objet en mouvement a parcouru, vous avez besoin pour trouver la distance entre deux objets fixes? Dans ce cas, la vitesse en fonction de la distance de la formule décrite ci-dessus ne sera pas de toute utilisation. Heureusement, une formule de la distance peut être utilisé pour trouver facilement la distance en ligne droite entre deux points. Toutefois, pour utiliser cette formule, vous aurez besoin de connaître les coordonnées de votre deux points. Si vous avez affaire à une dimension de la distance (comme sur un numéro de ligne), vos coordonnées seront deux nombres x1 et x2. Si vous faites affaire avec la distance en deux dimensions, vous aurez besoin de valeurs pour deux (x,y) des points (x1,y1) et (x2,y2). Enfin, pour les trois dimensions, vous aurez besoin de valeurs pour (x1,y1,z1) et (x2,y2,z2).
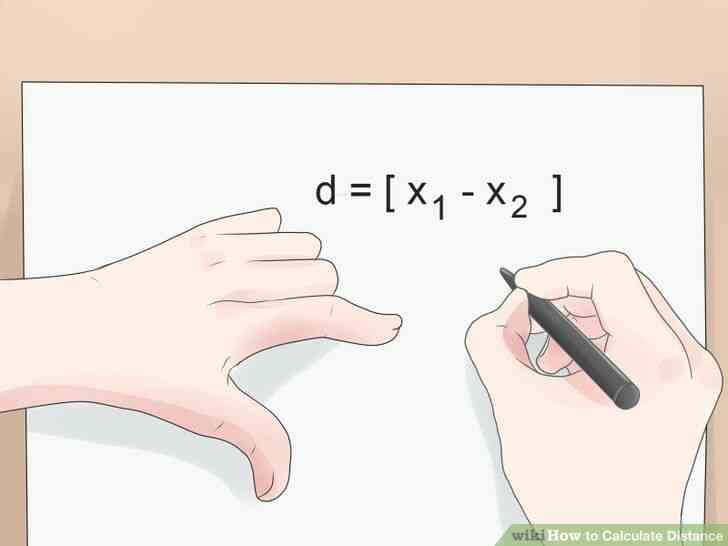
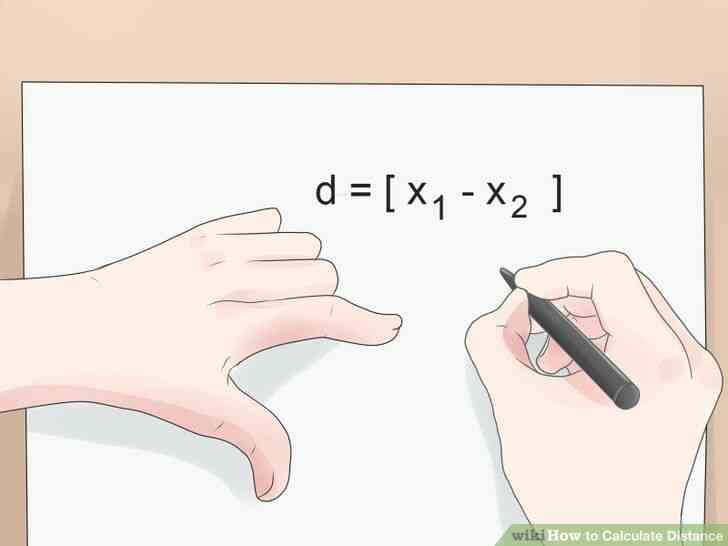
2
@@_
@@Trouver 1-D la distance en soustrayant la valeur des coordonnées des deux points. Le calcul unidimensionnel distance entre deux points lorsque vous connaissez la valeur de chacun est un jeu d'enfant. Tout simplement utiliser la formule d = |x2 - x1|. Dans cette formule, vous soustrayez x1 de x2, puis prendre la valeur absolue de votre réponse pour trouver la distance entre x1 et x2. Généralement, vous aurez envie d'utiliser le unidimensionnel formule de la distance lors de vos deux points se trouvent sur une ligne de nombre ou de l'axe.
- Notez que cette formule utilise des valeurs absolues (les '| |' symboles). Valeurs absolues signifie simplement que les termes contenus dans les symboles deviennent positifs si ils sont négatifs.
- Par exemple, disons que nous nous sommes arrêtés sur le bord de la route sur un parfaitement droit tronçon de l'autoroute. Si il est une petite ville, à 5 miles devant nous, et une ville de 1 mile derrière nous, à quelle distance sont les deux villes? Si nous mettons de ville 1 tel que x1 = 5 et de la ville, à 2 en tant que x1 = -1, on peut trouver d, la distance entre les deux villes, comme suit:
- d = |x2 - x1|
- =|-1 - 5|
- = |-6| = 6 milles.
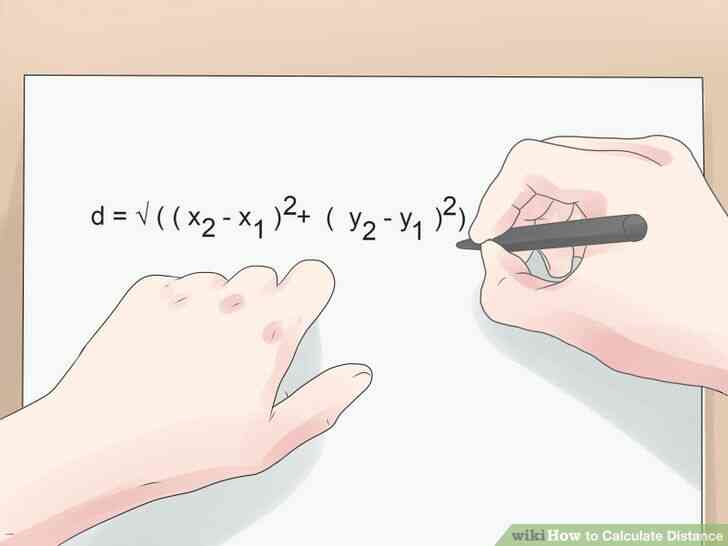
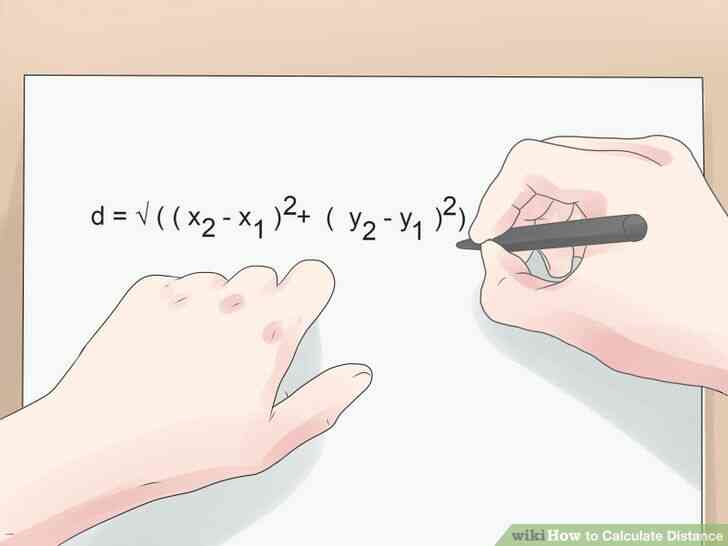
3
@@_
@@Trouver 2-D de la distance en utilisant le théorème de Pythagore. Trouver la distance entre deux points dans un espace à deux dimensions est plus compliqué que dans une seule dimension, mais il n'est pas difficile. Tout simplement utiliser la formule d = v((x2 - x1)2 (y2 - y1)2). Dans cette formule, vous soustrayez les deux coordonnées x, carré le résultat, de soustraire les coordonnées y, carré le résultat, puis ajouter les deux résultats intermédiaires ensemble et de prendre la racine carrée de trouver la distance entre vos deux points. Cette formule fonctionne dans le plan à deux dimensions, par exemple, sur la base de x/y de graphiques.
- 2-D de la formule de la distance de tire parti de la le théorème de Pythagore, qui dicte que l'hypoténuse d'un triangle rectangle est égal à la racine carrée des carrés des deux autres côtés.
- Par exemple, disons que nous avons deux points dans le plan x-y: (3, -10) et (11, 7) qui représentent le centre d'un cercle et un point sur le cercle, respectivement. Pour trouver la distance en ligne droite entre ces deux points, nous pouvons le résoudre comme suit:
- d = v((x2 - x1)2 (y2 - y1)2)
- d = v((11 - 3)2 (7 - -10)2)
- d = v(64 289)
- d = v(353) = 18.79
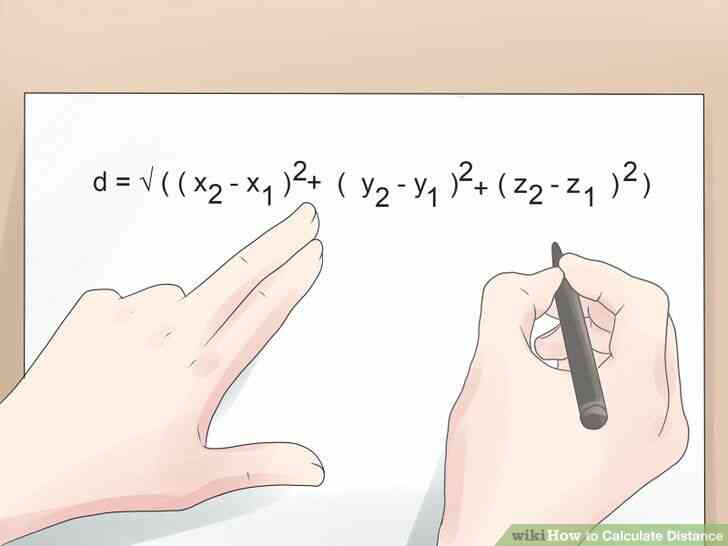
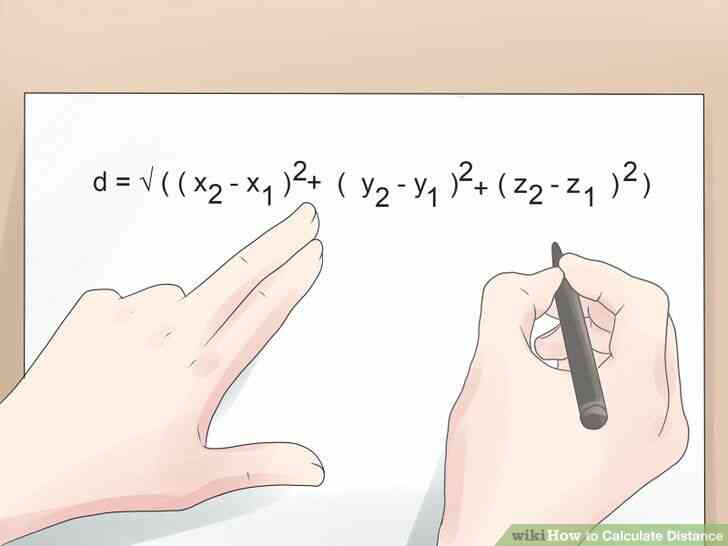
4
@@_
@@Trouver en 3-D de la distance par la modification de la 2-D de la formule. En trois dimensions, les points ont une coordonnée z en plus de leurs coordonnées x et y. Pour trouver la distance entre deux points dans l'espace à trois dimensions, l'utilisation d = v((x2 - x1)2 (y2 - y1)2 (z2 - z1)2). C'est une forme modifiée de la deux dimensions de la distance de la formule décrite ci-dessus qui prend le z coordonnées en compte. En soustrayant les deux z coordonnées, quadrature, et de procéder à travers le reste de la formule que ci-dessus vous assurer que votre réponse finale représente les trois dimensions de la distance entre vos deux points.
- Par exemple, disons que nous sommes un astronaute flottant dans l'espace près de deux astéroïdes. L'un est d'environ 8 kilomètres en face de nous, à 2 km à droite de nous, et à 5 miles au-dessous de nous, tandis que l'autre est à 3 km derrière nous, à 3 km à gauche de nous, et à 4 km au-dessus de nous. Si nous représentons les positions de ces astéroïdes avec les coordonnées (8,2,-5) et (-3,-3,4), nous pouvons trouver la distance entre les deux, comme suit:
- d = v((-3 - 8)2 (-3 - 2)2 (4 - -5)2)
- d = v((-11)2 (-5)2 (9)2)
- d = v(121 25 81)
- d = v(227) = 15.07 km
Comment Calculer la Distance
Distance, souvent assignee a la variable d, est une mesure de l'espace, contenue par une ligne droite entre deux points. La Distance peut se referer a l'espace entre les deux points stationnaires (par exemple, la taille d'une personne est la distance entre le dessous de ses pieds vers le haut de sa tete) ou peut se referer a l'espace entre la position actuelle d'un objet en mouvement et de son emplacement de depart. Plus la distance les problemes peuvent etre resolus avec les equations d = savg × t ou d est la distance, savg est la vitesse moyenne, et t est le temps, ou a l'aide d = √((x2 - x1)2 (y2 - y1)2), ou (x1, y1) et (x2, y2) sont les coordonnees x et y de deux points.
Mesures
@@_
@@
Methode 1
Trouver la Distance avec la Vitesse Moyenne et le Temps


1
@@_
@@Trouver les valeurs de vitesse moyenne et le temps. Lorsque vous essayez de trouver la distance d'un objet en mouvement a parcouru, deux informations sont essentielles pour faire ce calcul: sa vitesse (ou la vitesse de grandeur) et le temps qu'il a ete en mouvement. Avec cette information, il est possible de trouver la distance a laquelle l'objet a voyage a l'aide de la formule d = savg × t.
- Pour mieux comprendre le processus de l'aide de la formule de la distance, nous allons resoudre un exemple de probleme dans cette section. Disons que nous sommes devaler la route a 120 miles par heure (environ 193 km par heure) et nous voulons savoir ou nous allons nous rendre dans une demi-heure. A l'aide de 120 km / h comme notre valeur pour la vitesse moyenne et 0.5 heures que la valeur de notre temps, nous allons resoudre ce probleme dans la prochaine etape.


2
@@_
@@Multiplier la vitesse moyenne par heure. Une fois que vous connaissez la moyenne de la vitesse d'un objet en mouvement et le temps du voyage, trouver la distance qu'il a parcourue est relativement simple. Il suffit de multiplier ces deux quantites pour trouver votre reponse.
- Notez, cependant, que si les unites de temps utilisees dans votre moyenne de la valeur de la vitesse sont differentes de celles utilisees dans votre valeur de temps, vous aurez besoin de convertir un ou l'autre de sorte qu'ils sont compatibles. Par exemple, si nous avons une vitesse moyenne de la valeur qui est mesuree en km par heure et une valeur de temps est mesure en minutes, vous devez diviser la valeur de temps de 60 a convertir en heures.
- nous allons resoudre notre exemple de probleme. 120 km/h × 0,5 heure = 60 miles. Notez que les unites de la valeur de temps (heures) annuler avec les unites dans le denominateur de la vitesse moyenne (en heures) pour ne laisser que les unites de distance (miles).
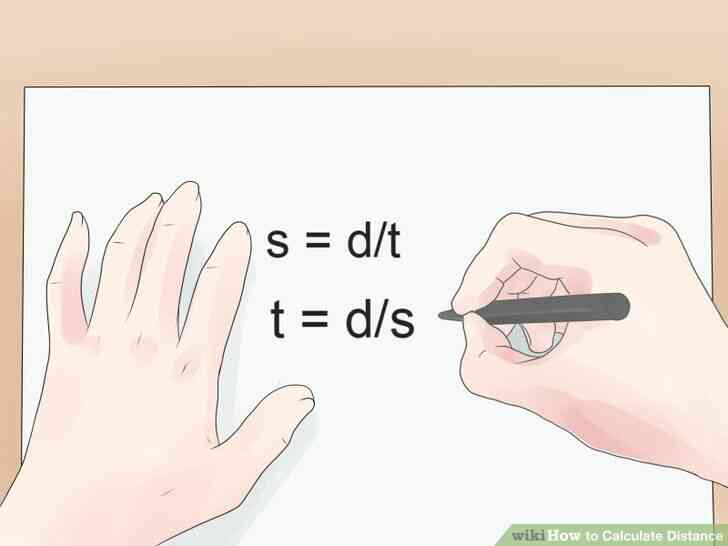
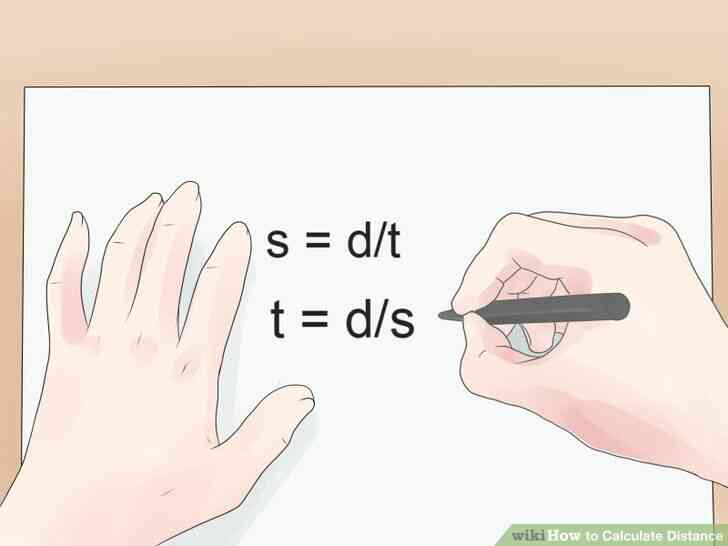
3
@@_
@@Manipuler l'equation a resoudre pour les autres variables. La simplicite de la base de la distance de l'equation (d = savg × t) le rend tres facile a utiliser l'equation pour trouver les valeurs des variables en plus de la distance. Simplement pour isoler la variable que vous voulez resoudre selon les regles de base de la algebre, puis inserez les valeurs de votre deux autres variables pour trouver la valeur de la troisieme. En d'autres termes, pour trouver l'objet de votre vitesse moyenne, l'utilisation de l'equation savg = d/t et a trouver a trouver le temps un objet a voyage, l'utilisation de l'equation t = d/savg.
- Par exemple, disons que nous savons qu'une voiture a conduit 60 km en 50 minutes, mais nous n'avons pas une valeur pour la vitesse moyenne lors d'un voyage. Dans ce cas, on peut isoler le savg variable dans la base de la distance de l'equation pour obtenir savg = d/t, alors il suffit de diviser 60 km / 50 minutes pour avoir une reponse de 1,2 miles/minute.
- a Noter que dans notre exemple, notre reponse pour la vitesse a une rare unites (km/minute). Pour obtenir votre reponse dans la forme la plus commune de miles/heure, de le multiplier par 60 minutes/heure pour atteindre 72 km/heure.


4
@@_
@@Remarque que le 'savg' variable dans la formule de la distance se refere a vitesse moyenne. Il est important de comprendre que la formule de la distance offre une vue simplifiee du mouvement d'un objet. La formule de la distance suppose que l'objet en mouvement a une vitesse constante — en d'autres termes, on suppose que l'objet en mouvement se deplace a une unique, immuable taux de vitesse. Pour les mathematiques abstraites, des problemes, tels que ceux que vous pouvez rencontrer dans un cadre academique, c'est parfois encore possible de modeliser un objet en mouvement a l'aide de cette hypothese. Dans la vraie vie, cependant, ce modele n'est souvent pas refleter avec precision le mouvement des objets en mouvement, ce qui peut, en realite, accelerer, ralentir, arreter et inverser le cours du temps.
- Par exemple, dans l'exemple ci-dessus, nous avons conclu que le voyage de 60 km en 50 minutes, nous aurions besoin de voyager a 72 km/heure. Cependant, cela n'est vrai que si le voyage a une vitesse pour la totalite du voyage. Par exemple, en voyageant a 80 km/h pour la moitie du voyage et de 64 km/heure pour l'autre moitie, on va encore en voyage de 60 km en 50 minutes — 72 milles/heure = 60 km/50 min. = ?????
- Calcul de solutions a base d' l'utilisation d'instruments derives sont souvent un meilleur choix que la formule de la distance pour la definition d'un objet de la vitesse dans les situations du monde reel parce que les changements de vitesse sont susceptibles.
@@_
@@
Methode 2
Trouver la Distance entre Deux Points
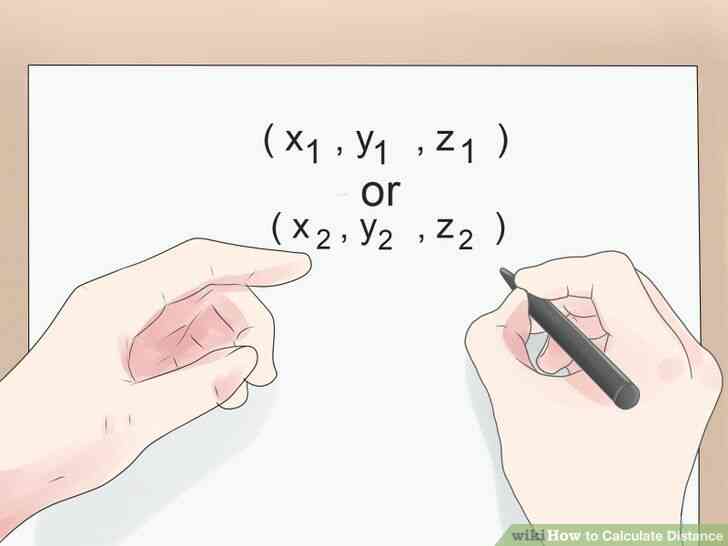
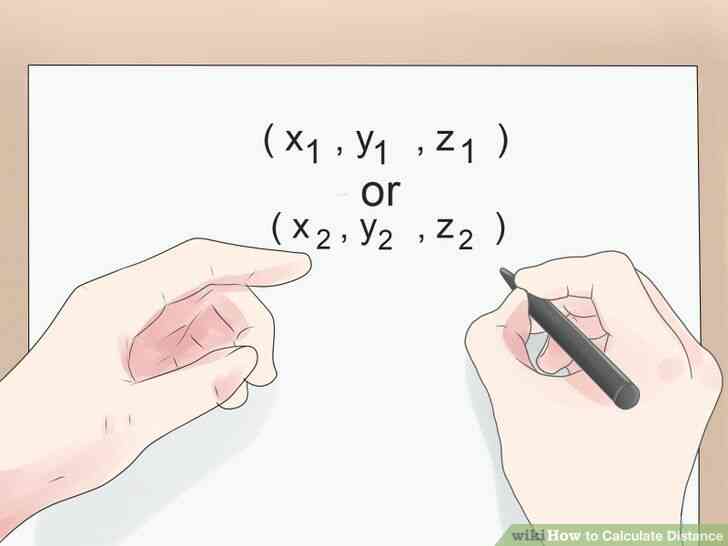
1
@@_
@@Trouver deux points de coordonnees spatiales. Et si, plutot que de trouver la distance d'un objet en mouvement a parcouru, vous avez besoin pour trouver la distance entre deux objets fixes? Dans ce cas, la vitesse en fonction de la distance de la formule decrite ci-dessus ne sera pas de toute utilisation. Heureusement, une formule de la distance peut etre utilise pour trouver facilement la distance en ligne droite entre deux points. Toutefois, pour utiliser cette formule, vous aurez besoin de connaître les coordonnees de votre deux points. Si vous avez affaire a une dimension de la distance (comme sur un numero de ligne), vos coordonnees seront deux nombres x1 et x2. Si vous faites affaire avec la distance en deux dimensions, vous aurez besoin de valeurs pour deux (x,y) des points (x1,y1) et (x2,y2). Enfin, pour les trois dimensions, vous aurez besoin de valeurs pour (x1,y1,z1) et (x2,y2,z2).
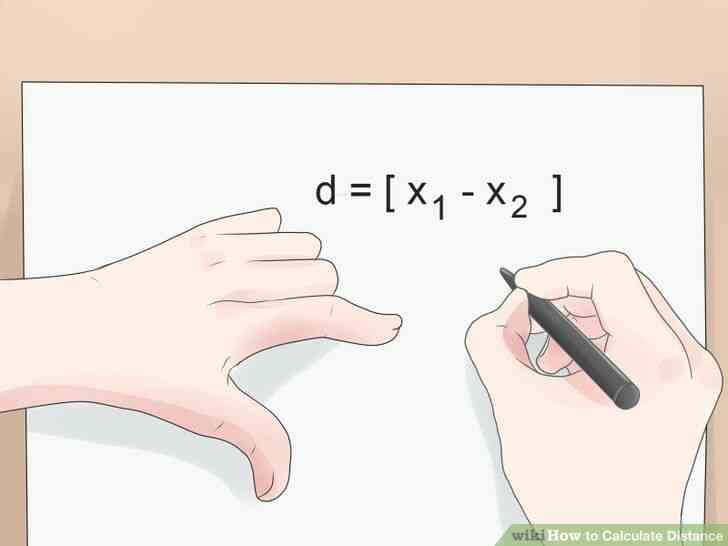
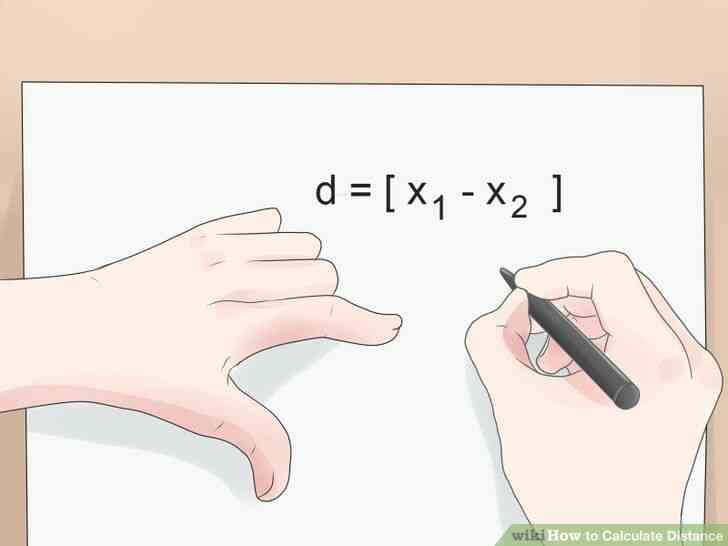
2
@@_
@@Trouver 1-D la distance en soustrayant la valeur des coordonnees des deux points. Le calcul unidimensionnel distance entre deux points lorsque vous connaissez la valeur de chacun est un jeu d'enfant. Tout simplement utiliser la formule d = |x2 - x1|. Dans cette formule, vous soustrayez x1 de x2, puis prendre la valeur absolue de votre reponse pour trouver la distance entre x1 et x2. Generalement, vous aurez envie d'utiliser le unidimensionnel formule de la distance lors de vos deux points se trouvent sur une ligne de nombre ou de l'axe.
- Notez que cette formule utilise des valeurs absolues (les '| |' symboles). Valeurs absolues signifie simplement que les termes contenus dans les symboles deviennent positifs si ils sont negatifs.
- Par exemple, disons que nous nous sommes arretes sur le bord de la route sur un parfaitement droit tronçon de l'autoroute. Si il est une petite ville, a 5 miles devant nous, et une ville de 1 mile derriere nous, a quelle distance sont les deux villes? Si nous mettons de ville 1 tel que x1 = 5 et de la ville, a 2 en tant que x1 = -1, on peut trouver d, la distance entre les deux villes, comme suit:
- d = |x2 - x1|
- =|-1 - 5|
- = |-6| = 6 milles.
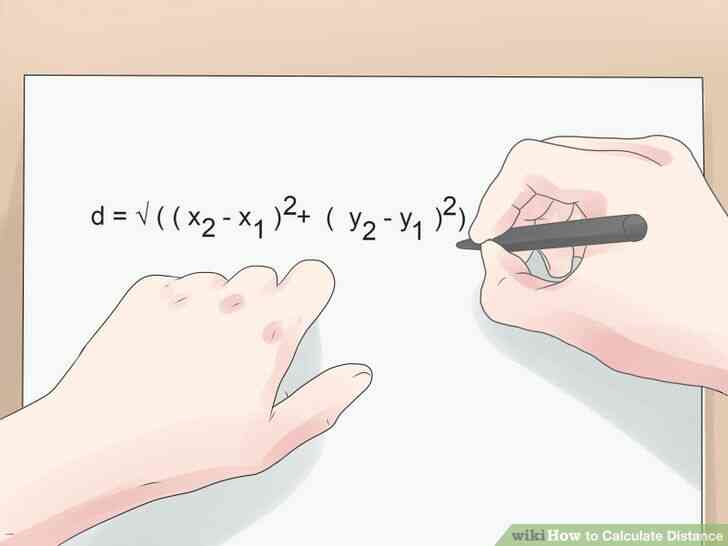
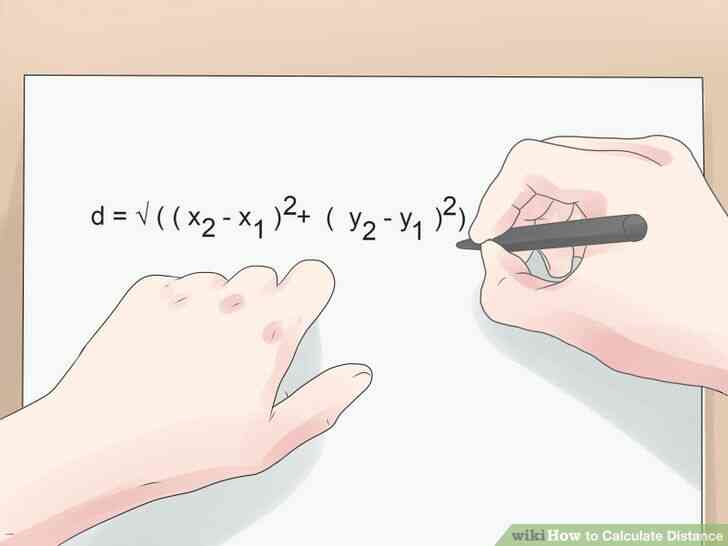
3
@@_
@@Trouver 2-D de la distance en utilisant le theoreme de Pythagore. Trouver la distance entre deux points dans un espace a deux dimensions est plus complique que dans une seule dimension, mais il n'est pas difficile. Tout simplement utiliser la formule d = v((x2 - x1)2 (y2 - y1)2). Dans cette formule, vous soustrayez les deux coordonnees x, carre le resultat, de soustraire les coordonnees y, carre le resultat, puis ajouter les deux resultats intermediaires ensemble et de prendre la racine carree de trouver la distance entre vos deux points. Cette formule fonctionne dans le plan a deux dimensions, par exemple, sur la base de x/y de graphiques.
- 2-D de la formule de la distance de tire parti de la le theoreme de Pythagore, qui dicte que l'hypotenuse d'un triangle rectangle est egal a la racine carree des carres des deux autres cotes.
- Par exemple, disons que nous avons deux points dans le plan x-y: (3, -10) et (11, 7) qui representent le centre d'un cercle et un point sur le cercle, respectivement. Pour trouver la distance en ligne droite entre ces deux points, nous pouvons le resoudre comme suit:
- d = v((x2 - x1)2 (y2 - y1)2)
- d = v((11 - 3)2 (7 - -10)2)
- d = v(64 289)
- d = v(353) = 18.79
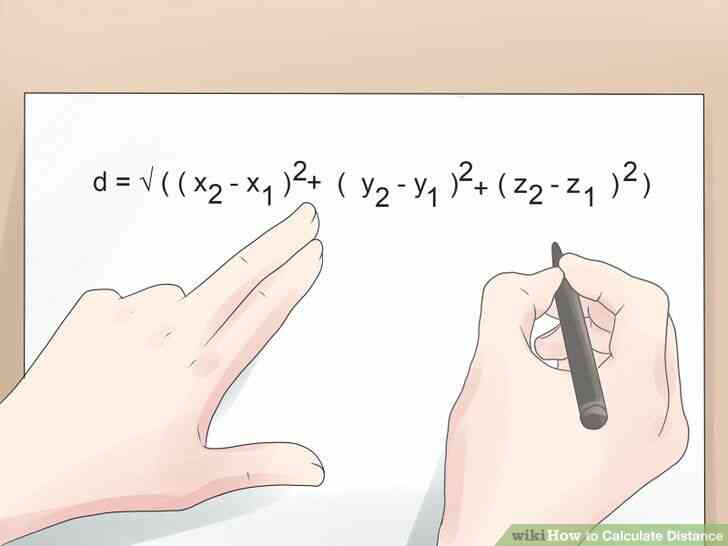
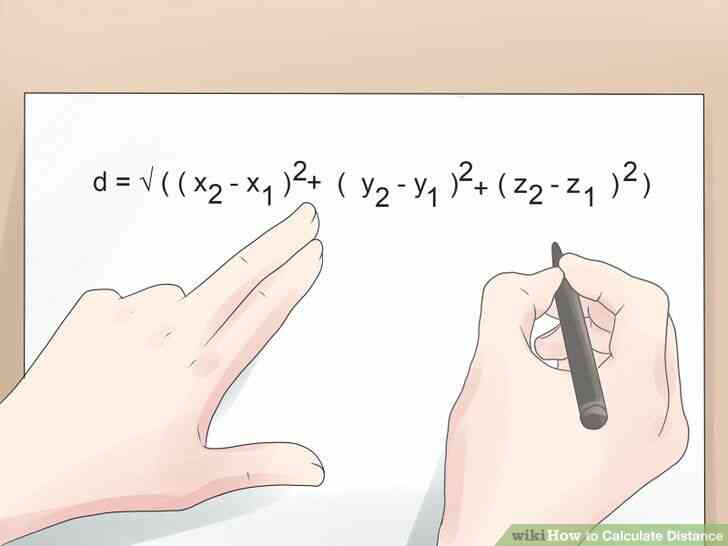
4
@@_
@@Trouver en 3-D de la distance par la modification de la 2-D de la formule. En trois dimensions, les points ont une coordonnee z en plus de leurs coordonnees x et y. Pour trouver la distance entre deux points dans l'espace a trois dimensions, l'utilisation d = v((x2 - x1)2 (y2 - y1)2 (z2 - z1)2). C'est une forme modifiee de la deux dimensions de la distance de la formule decrite ci-dessus qui prend le z coordonnees en compte. En soustrayant les deux z coordonnees, quadrature, et de proceder a travers le reste de la formule que ci-dessus vous assurer que votre reponse finale represente les trois dimensions de la distance entre vos deux points.
- Par exemple, disons que nous sommes un astronaute flottant dans l'espace pres de deux asteroïdes. L'un est d'environ 8 kilometres en face de nous, a 2 km a droite de nous, et a 5 miles au-dessous de nous, tandis que l'autre est a 3 km derriere nous, a 3 km a gauche de nous, et a 4 km au-dessus de nous. Si nous representons les positions de ces asteroïdes avec les coordonnees (8,2,-5) et (-3,-3,4), nous pouvons trouver la distance entre les deux, comme suit:
- d = v((-3 - 8)2 (-3 - 2)2 (4 - -5)2)
- d = v((-11)2 (-5)2 (9)2)
- d = v(121 25 81)
- d = v(227) = 15.07 km
Comment Calculer la Distance
By commentfaire
Distance, souvent assignée à la variable d, est une mesure de l'espace, contenue par une ligne droite entre deux points. La Distance peut se référer à l'espace entre les deux points stationnaires (par exemple, la taille d'une personne est la distance entre le dessous de ses pieds vers le haut de sa tête) ou peut se référer à l'espace entre la position actuelle d'un objet en mouvement et de son emplacement de départ. Plus la distance les problèmes peuvent être résolus avec les équations d = savg × t où d est la distance, savg est la vitesse moyenne, et t est le temps, ou à l'aide d = √((x2 - x1)2 (y2 - y1)2), où (x1, y1) et (x2, y2) sont les coordonnées x et y de deux points.