Factorielles, notée par un !{\displaystyle !} signe, sont les produits d'un nombre entier et de tous les nombres entiers ci-dessous. Il est facile de calculer et de multiplier deux factorielles à l'aide d'une calculatrice scientifique du x!{\displaystyle x!} fonction. Vous pouvez aussi multiplier les factorielles à la main. La façon la plus simple de le faire est de calculer, pour chaque factorielle individuellement, puis à multiplier leurs produits. Vous pouvez également utiliser certaines règles de factorielles de sortir de facteurs communs, ce qui peut simplifier le processus de multiplication.
Mesures
@@_
@@
Méthode 1
Comprendre les Factorielles
1
@@_
@@Identifier une factorielle. Une factorielle, caractérisée par un grand nombre avec un point d'exclamation, est le produit d'une série de séquentielles des nombres entiers.[1]
- Par exemple, les 6!{\displaystyle 6!} est factoriel.
2
@@_
@@Évaluer une factorielle à l'aide d'une formule. La formule est n!=n(n-1)(n-2)···3·2·1{\displaystyle n!=n(n-1)(n-2)\cdot \cdot \cdot 3\cdot 2\cdot 1}.[2] Cela signifie que vous étendez la séquence de nombres jusqu'à 1.
- Par exemple, 6!=6(6-1)(6-2)(6-3)(6-4)(6-5)=6(5)(4)(3)(2)(1){\displaystyle 6!=6(6-1)(6-2)(6-3)(6-4)(6-5)=6(5)(4)(3)(2)(1)}
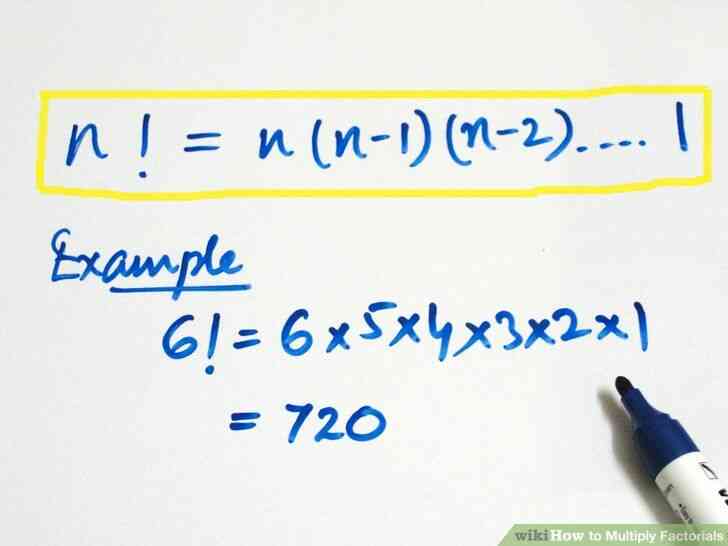
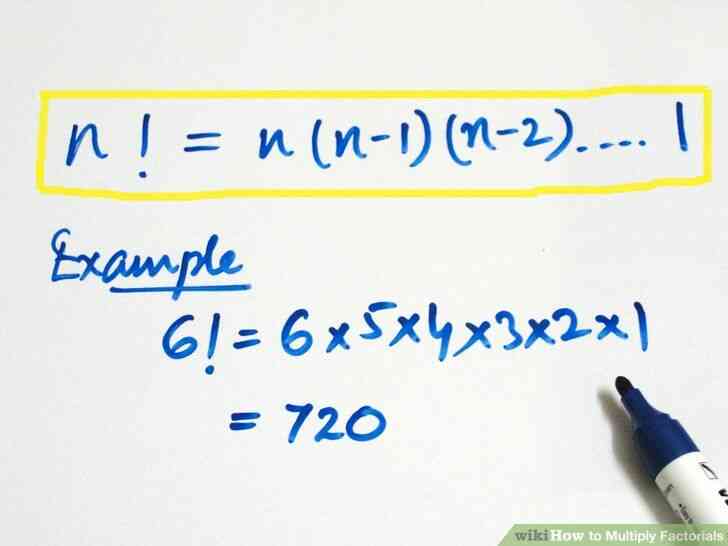
3
@@_
@@Calculer une factorielle. Pour calculer une factorielle, commencer avec l'notée nombre, et de le multiplier par chaque séquence de nombre entier, jusqu'à 1.[3] Un moyen rapide de calculer une factorielle est d'utiliser le x!{\displaystyle x!} sur une calculatrice scientifique. D'abord taper le numéro, puis appuyez sur le x!{\displaystyle x!} touche pour voir le produit.
- Par exemple, 6!=6×5×4×3×2×1=720{\displaystyle 6!=6\times 5\times 4\times 3\times 2\times 1=720}.
@@_
@@
Méthode 2
Calculer les Factorielles Séparément
1
@@_
@@Calculer le premier factorielle. L'utilisation d'une calculatrice pour le plus grand nombre. Si le calcul à la main, assurez-vous de multiplier chaque numéro séquentiel, jusqu'à 1. Réécrire l'équation avec ce produit, entre parenthèses, que le premier facteur.
- Par exemple, si vous effectuez le calcul des 5!×7!{\displaystyle 5!\fois 7!}, tout d'abord calculer 5!{\displaystyle 5!}:5!×7!{\displaystyle 5!\fois 7!}=(5×4×3×2×1)×(7!){\displaystyle =(5\times 4\times 3\times 2\times 1)\times (7!)}=(120)×(7!){\displaystyle =(120)\times (7!)}
2
@@_
@@Calculer le deuxième factorielle. Vous pouvez le faire par calculateur ou à la main, à compter de la complexité de la factorielle. Réécrire l'équation avec ce produit comme le deuxième facteur.
- Par exemple:(120)×(7!){\displaystyle (120)\times (7!)}=(120)×(7×6×5×4×3×2×1){\displaystyle =(120)\times (7\times 6\times 5\times 4\times 3\times 2\times 1)}=(120)×(5040){\displaystyle =(120)\times (5040)}
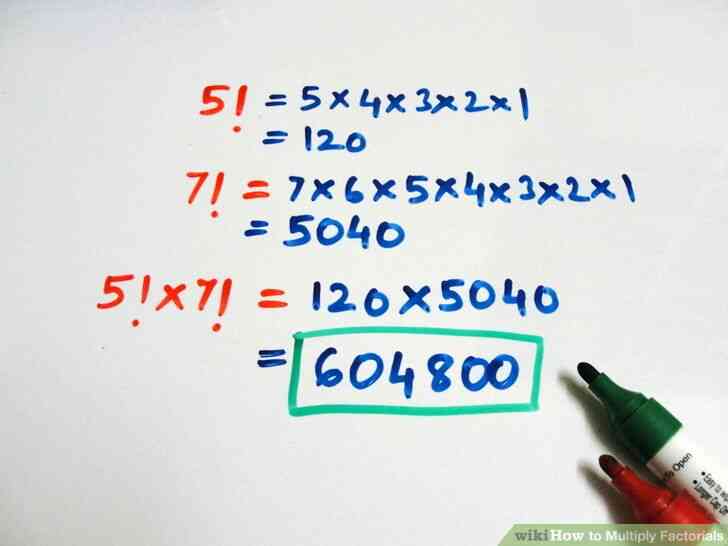
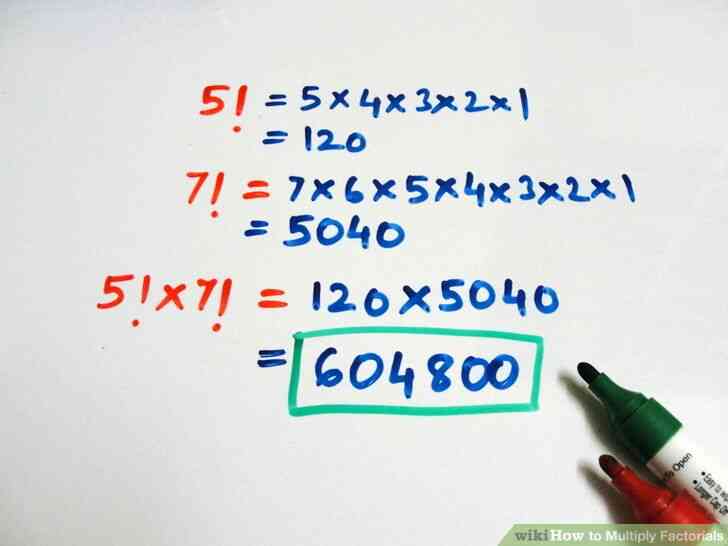
3
@@_
@@Multipliez les deux factorielles produits. Cela vous donnera le produit des deux factorielles. Depuis factorielles ont tendance à être grand nombre, à l'aide d'une calculatrice va faire ce calcul plus facile.
- Par exemple, (120)×(5040)=604,800{\displaystyle (120)\times (5040)=604,800}. Donc, 5!×7!=604,800{\displaystyle 5!\fois 7!=604,800}.
@@_
@@
Méthode 3
Trouver des Facteurs Communs
1
@@_
@@Utiliser une formule pour le facteur de la plus grande commune de la factorielle. La formule est n!=n×(n-1)!{\displaystyle n!=n\times (n-1)!}. Cela signifie qu'une plus petite factorielle est un facteur d'une plus grande factorielle.[4] Par exemple, 4!=4×(4-1)!=4×3!{\displaystyle 4!=4\times (4-1)!=4\times 3!}. Lorsque vous êtes à la multiplication de deux factorielles, la plus grande commune de la factorielle est la plus petite des deux factorielles.
- Par exemple, si vous effectuez le calcul des 5!×7!{\displaystyle 5!\fois 7!}, vous pouvez le facteur 5!{\displaystyle 5!} à partir de 7!{\displaystyle 7!}:5!×5!(7×6){\displaystyle 5!\fois sur 5!(7\times 6)}
2
@@_
@@Réécrire l'équation, montrant la commune factorielle comme un carré de la valeur. Ensuite, calculer la factorielle et de carrés de ses produits.
- Par exemple, 5!×5!(7×6){\displaystyle 5!\fois sur 5!(7\times 6)}=7×6×(5!)2{\displaystyle =7\times 6\times (5!)^{2}}=42×(120)2{\displaystyle =42\times (120)^{2}}
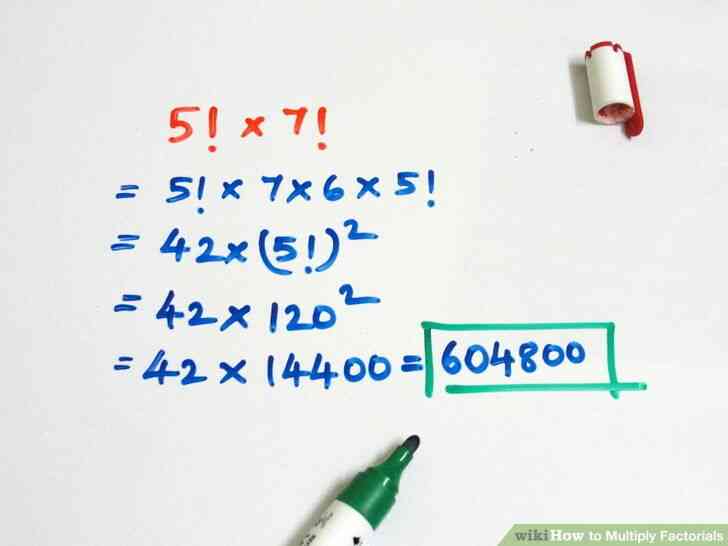
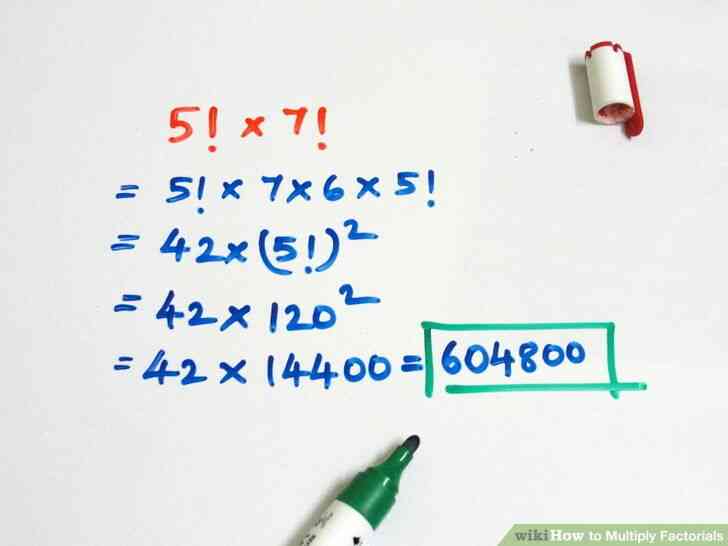
3
@@_
@@Multipliez les autres facteurs. Le résultat sera le produit des deux premières factorielles.
- Par exemple: 42×(120)2{\displaystyle 42\times (120)^{2}}=42×14,400{\displaystyle =42\times de 14 400}=604,800{\displaystyle =604,800}
Comment Multiplier les Factorielles
Factorielles, notee par un !{\displaystyle !} signe, sont les produits d'un nombre entier et de tous les nombres entiers ci-dessous. Il est facile de calculer et de multiplier deux factorielles a l'aide d'une calculatrice scientifique du x!{\displaystyle x!} fonction. Vous pouvez aussi multiplier les factorielles a la main. La façon la plus simple de le faire est de calculer, pour chaque factorielle individuellement, puis a multiplier leurs produits. Vous pouvez egalement utiliser certaines regles de factorielles de sortir de facteurs communs, ce qui peut simplifier le processus de multiplication.
Mesures
@@_
@@
Methode 1
Comprendre les Factorielles
1
@@_
@@Identifier une factorielle. Une factorielle, caracterisee par un grand nombre avec un point d'exclamation, est le produit d'une serie de sequentielles des nombres entiers.[1]
- Par exemple, les 6!{\displaystyle 6!} est factoriel.
2
@@_
@@Evaluer une factorielle a l'aide d'une formule. La formule est n!=n(n-1)(n-2)···3·2·1{\displaystyle n!=n(n-1)(n-2)\cdot \cdot \cdot 3\cdot 2\cdot 1}.[2] Cela signifie que vous etendez la sequence de nombres jusqu'a 1.
- Par exemple, 6!=6(6-1)(6-2)(6-3)(6-4)(6-5)=6(5)(4)(3)(2)(1){\displaystyle 6!=6(6-1)(6-2)(6-3)(6-4)(6-5)=6(5)(4)(3)(2)(1)}
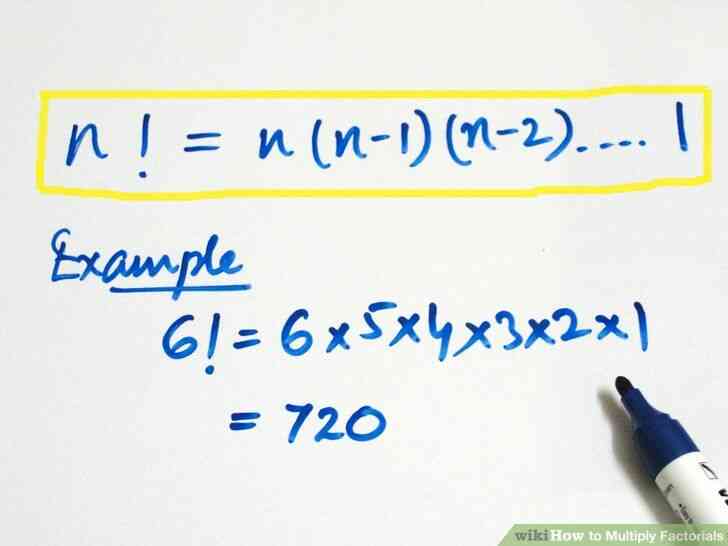
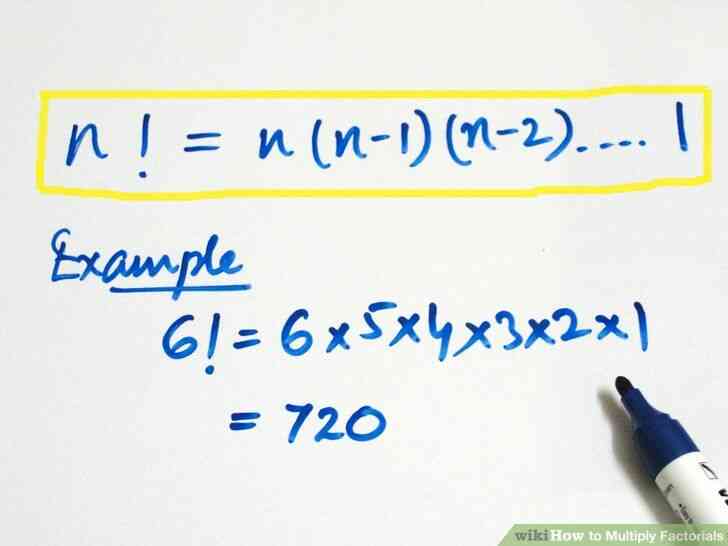
3
@@_
@@Calculer une factorielle. Pour calculer une factorielle, commencer avec l'notee nombre, et de le multiplier par chaque sequence de nombre entier, jusqu'a 1.[3] Un moyen rapide de calculer une factorielle est d'utiliser le x!{\displaystyle x!} sur une calculatrice scientifique. D'abord taper le numero, puis appuyez sur le x!{\displaystyle x!} touche pour voir le produit.
- Par exemple, 6!=6×5×4×3×2×1=720{\displaystyle 6!=6\times 5\times 4\times 3\times 2\times 1=720}.
@@_
@@
Methode 2
Calculer les Factorielles Separement
1
@@_
@@Calculer le premier factorielle. L'utilisation d'une calculatrice pour le plus grand nombre. Si le calcul a la main, assurez-vous de multiplier chaque numero sequentiel, jusqu'a 1. Reecrire l'equation avec ce produit, entre parentheses, que le premier facteur.
- Par exemple, si vous effectuez le calcul des 5!×7!{\displaystyle 5!\fois 7!}, tout d'abord calculer 5!{\displaystyle 5!}:5!×7!{\displaystyle 5!\fois 7!}=(5×4×3×2×1)×(7!){\displaystyle =(5\times 4\times 3\times 2\times 1)\times (7!)}=(120)×(7!){\displaystyle =(120)\times (7!)}
2
@@_
@@Calculer le deuxieme factorielle. Vous pouvez le faire par calculateur ou a la main, a compter de la complexite de la factorielle. Reecrire l'equation avec ce produit comme le deuxieme facteur.
- Par exemple:(120)×(7!){\displaystyle (120)\times (7!)}=(120)×(7×6×5×4×3×2×1){\displaystyle =(120)\times (7\times 6\times 5\times 4\times 3\times 2\times 1)}=(120)×(5040){\displaystyle =(120)\times (5040)}
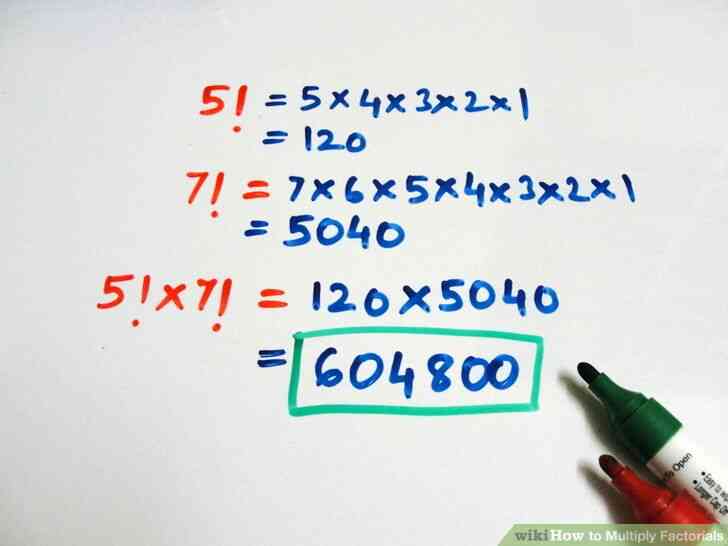
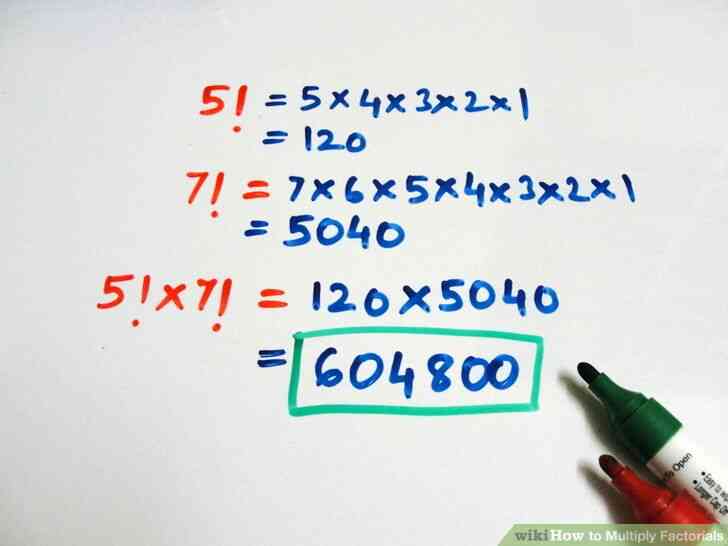
3
@@_
@@Multipliez les deux factorielles produits. Cela vous donnera le produit des deux factorielles. Depuis factorielles ont tendance a etre grand nombre, a l'aide d'une calculatrice va faire ce calcul plus facile.
- Par exemple, (120)×(5040)=604,800{\displaystyle (120)\times (5040)=604,800}. Donc, 5!×7!=604,800{\displaystyle 5!\fois 7!=604,800}.
@@_
@@
Methode 3
Trouver des Facteurs Communs
1
@@_
@@Utiliser une formule pour le facteur de la plus grande commune de la factorielle. La formule est n!=n×(n-1)!{\displaystyle n!=n\times (n-1)!}. Cela signifie qu'une plus petite factorielle est un facteur d'une plus grande factorielle.[4] Par exemple, 4!=4×(4-1)!=4×3!{\displaystyle 4!=4\times (4-1)!=4\times 3!}. Lorsque vous etes a la multiplication de deux factorielles, la plus grande commune de la factorielle est la plus petite des deux factorielles.
- Par exemple, si vous effectuez le calcul des 5!×7!{\displaystyle 5!\fois 7!}, vous pouvez le facteur 5!{\displaystyle 5!} a partir de 7!{\displaystyle 7!}:5!×5!(7×6){\displaystyle 5!\fois sur 5!(7\times 6)}
2
@@_
@@Reecrire l'equation, montrant la commune factorielle comme un carre de la valeur. Ensuite, calculer la factorielle et de carres de ses produits.
- Par exemple, 5!×5!(7×6){\displaystyle 5!\fois sur 5!(7\times 6)}=7×6×(5!)2{\displaystyle =7\times 6\times (5!)^{2}}=42×(120)2{\displaystyle =42\times (120)^{2}}
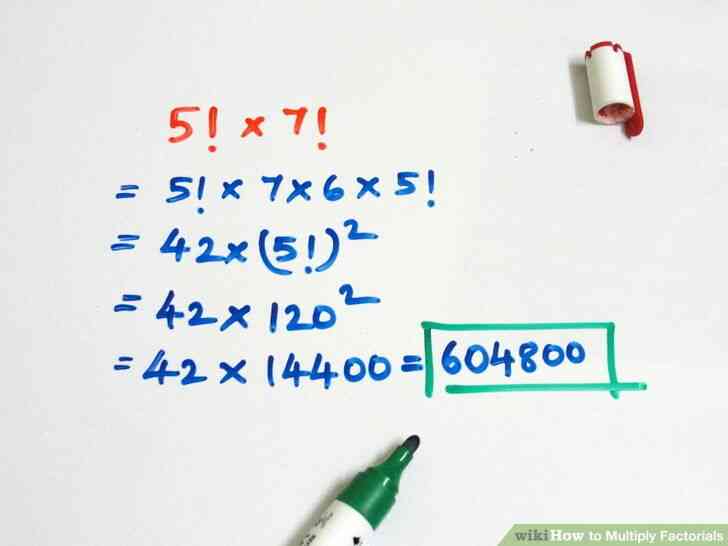
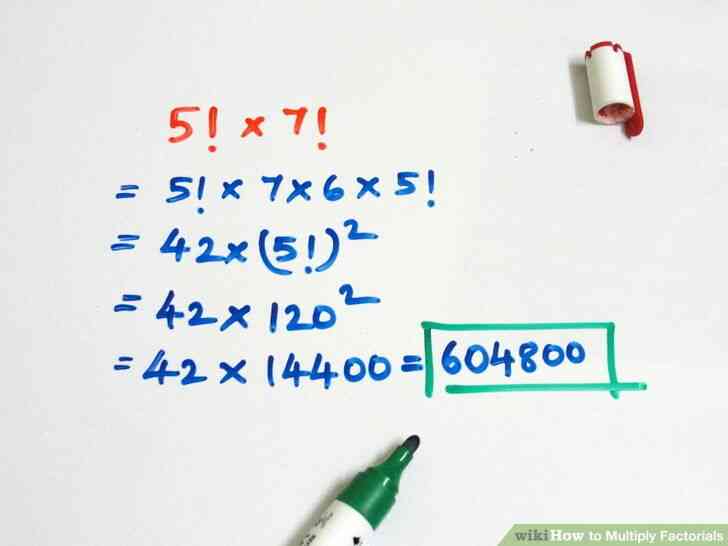
3
@@_
@@Multipliez les autres facteurs. Le resultat sera le produit des deux premieres factorielles.
- Par exemple: 42×(120)2{\displaystyle 42\times (120)^{2}}=42×14,400{\displaystyle =42\times de 14 400}=604,800{\displaystyle =604,800}
Comment Multiplier les Factorielles
By commentfaire
Factorielles, notée par un !{\displaystyle !} signe, sont les produits d'un nombre entier et de tous les nombres entiers ci-dessous. Il est facile de calculer et de multiplier deux factorielles à l'aide d'une calculatrice scientifique du x!{\displaystyle x!} fonction. Vous pouvez aussi multiplier les factorielles à la main. La façon la plus simple de le faire est de calculer, pour chaque factorielle individuellement, puis à multiplier leurs produits. Vous pouvez également utiliser certaines règles de factorielles de sortir de facteurs communs, ce qui peut simplifier le processus de multiplication.