En physique, la tension est la force exercée par une corde, une chaîne, un câble ou tout autre objet similaire sur un ou plusieurs objets. Rien retiré, suspendu, prise en charge, ou en passant d'une corde, chaîne, câble, etc. est soumis à la force de tension. Comme toutes les forces, les tensions peuvent accélérer objets ou de provoquer une déformation. Être capable de calculer la tension est une compétence importante non seulement pour les étudiants en physique, mais aussi pour les ingénieurs et les architectes, qui, à construire des bâtiments sûrs, doit savoir si la tension sur une corde ou d'un câble peut résister à la déformation causée par le poids de l'objet avant de céder et de se casser. Voir l'Étape 1 pour savoir comment calculer la tension dans plusieurs systèmes physiques.
Mesures
@@_
@@
Méthode 1
Détermination de la Tension Sur un Seul Brin


1
@@_
@@Définir les forces sur l'une des extrémités de la fibre. La tension dans un brin de ficelle ou de la corde est le résultat des forces de traction sur la corde de chaque extrémité. Pour rappel, force = masse × accélération. En supposant que la corde est tendue, tout changement de l'accélération ou de masse dans les objets de la corde soutient va provoquer un changement dans la tension dans la corde. Ne pas oublier la constante d'accélération due à la gravité (même si un système est au repos, ses composants sont soumis à cette force. Nous pouvons penser à une tension dans la corde que T = (m × g) (m × a), où 'g' est l'accélération due à la gravité de tous les objets de la corde est de soutenir et de 'une' est tout autre accélération sur tous les objets de la corde soutient.
- Pour les besoins de la plupart des problèmes de physique, nous supposons idéal cordes - en d'autres termes, que notre corde, câble, etc. est mince, de masse nulle, et ne peut pas être étiré ou cassé.
- Comme un exemple, considérons un système où un poids suspendu à une poutre de bois par l'intermédiaire d'un seul câble (voir photo). Ni le poids ni la corde sont en mouvement l'ensemble du système est au repos. De ce fait, nous savons que, pour le poids d'être tenue dans l'équilibre, la force de tension doit être égale à la force de gravité sur le poids. En d'autres termes, la Tension (Ft) = Force de gravité (Fg) = m × g.
- en Supposant une 10 kg de poids, alors, la force de tension est de 10 kg × 9,8 m/s2 = 98 Newtons.


2
@@_
@@Compte pour l'accélération. La gravité n'est pas la seule force qui peut affecter la tension d'une corde - alors, peut-toute la force liée à l'accélération d'un objet, la corde est attachée. Si, par exemple, une suspension de l'objet est accéléré par une force sur la corde ou le câble, la force d'accélération (masse × accélération) est ajoutée à la tension provoquée par le poids de l'objet.
- disons que, dans notre exemple de l'10 kg de poids suspendu par une corde, qui, au lieu d'être fixé à une poutre de bois, la corde est effectivement utilisé pour tirer le poids vers le haut à une accélération de 1 m/s2. Dans ce cas, nous devons tenir compte de l'accélération sur le poids ainsi que la force de gravité par la résolution comme suit:
- Pi = Fg m × a
- Pi = 98 10 kg × 1 m/s2
- Pi = 108 Newtons.

3
@@_
@@Compte pour l'accélération de rotation. Un objet en rotation autour d'un point central au moyen d'une corde (comme un pendule) exerce une pression sur la corde causée par la force centripète. La force centripète est ajoutée force de tension de la corde exerce en 'tirant' vers l'intérieur pour garder un objet en mouvement dans l'arc et non pas en ligne droite. Plus l'objet est en mouvement, plus grande est la force centripète. La force centripète (Fc) est égal à m × v2/r, où 'm' est la masse, le 'v' est la vitesse, et 'r' est le rayon du cercle qui contient l'arc de mouvement de l'objet.
- Depuis la direction et l'amplitude de la force centripète changements que l'objet sur la corde, les déplacements et les changements de vitesses, de sorte que le total de la tension dans la corde, qui tire toujours parallèle à la corde vers le point central. Rappelez-vous aussi que la force de gravité est constamment en agissant sur l'objet dans une direction vers le bas. Donc, si un objet est en train de provoquer ou basculé à la verticale, le total de la tension est au plus bas de l'arc (pour un pendule, ce qui est appelé le point d'équilibre) lorsque l'objet est en mouvement plus rapide et la moins au sommet de l'arc lorsqu'il est en mouvement plus lent.
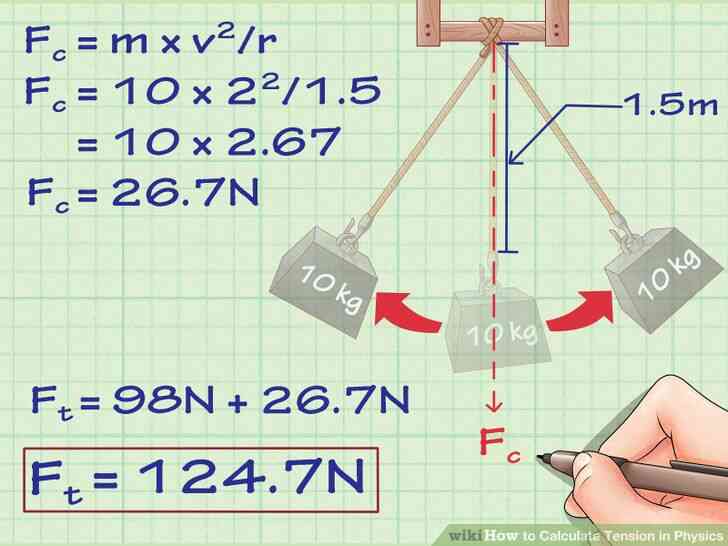
- disons que dans notre exemple, le problème que notre objet n'est plus l'accélération de la hausse, mais au lieu de se balancer comme un pendule. On va dire que notre corde de 1,5 m (4,9 pi) de long et que notre poids se déplace à 2 m/s lorsqu'il passe à travers le fond de son swing. Si nous voulons calculer la tension à la partie inférieure de l'arc lorsqu'il est plus haut, il faudrait d'abord reconnaître que la tension due à la gravité, à ce point est le même que lorsque le poids était tenu immobile - 98 Newtons.Afin de trouver le supplément de la force centripète, nous permettrait de résoudre comme suit:
- Fc = m × v2/r
- Fc = 10 × 22/1.5
- Fc =10 × 2.67 = 26.7 Newtons.
- Donc, notre le total de la tension serait de 98 à 26,7 = 124.7 Newtons.


4
@@_
@@Comprendre que la tension due à la gravité des changements tout au long d'un balancement de l'objet à l'arc. Comme indiqué ci-dessus, à la fois la direction et l'amplitude de la force centripète le changement comme un objet de balançoires. Cependant, bien que la force de gravité qui reste constant, la tension qui résulte de la gravité change également. Quand le swing d'un objet n'est pas au fond de son arc (son point d'équilibre), la gravité est en tirant directement vers le bas, mais la tension est de tirer vers le haut à un angle. De ce fait, la tension n'a qu'à neutraliser une partie de la force due à la gravité, plutôt que de son intégralité.
- Rupture de la force gravitationnelle entre deux vecteurs peuvent vous aider à visualiser ce concept. À un moment donné dans l'arc de la verticale à balancer de l'objet, de la corde forme un angle '?', avec la ligne passant par le point d'équilibre et le point central de rotation. Comme le pendule, la force gravitationnelle (m × g) peut être décomposé en deux vecteurs - mgsin(?) en agissant de la tangente à l'arc dans la direction du point d'équilibre et mgcos(?) agissant en parallèle à la force de tension dans la direction opposée. La Tension n'a qu'à contre mgcos(?) - la force qui attire contre elle - et non l'ensemble de la force gravitationnelle (sauf au point d'équilibre, lorsque ceux-ci sont égaux).
- disons que lorsque notre pendule forme un angle de 15 degrés avec la verticale, il se déplace à 1,5 m/s. Nous trouverions de la tension par la résolution comme suit:
- Tension due à la gravité (Tg) = 98cos(15) = 98(0.96) = 94.08 Newton
- la force Centripète (Fc) = 10 × 1.52/1.5 = 10 × 1.5 = 15 Newton
- Total tension = Tg Fc = 94.08 15 = 109.08 Newtons.


5
@@_
@@Compte pour le frottement. Tout objet tiré par une corde que l'expérience d'un 'glisser' de la force de friction contre un autre objet (ou fluide) les transferts de cette force de la tension dans la corde. La Force de frottement entre les deux objets est calculé comme dans toute autre situation - par l'équation suivante: Force due à la friction (généralement écrites Fr) = (mu)N, où mu est le coefficient de frottement entre les deux objets et N est la normale à la force entre les deux objets, ou la force avec laquelle ils sont en appuyant les uns les autres. Notez que le frottement statique - la friction que les résultats lorsque vous essayez de mettre un objet à l'arrêt en mouvement est différent de celui de frottement le frottement que les résultats en essayant de garder un objet en mouvement en mouvement.
- disons que l'une de nos 10 kg de poids n'est plus balancé, mais est maintenant déplacée horizontalement sur le sol par notre corde. Disons que le sol a un coefficient de frottement cinétique entre 0,5 et que notre poids se déplace à une vitesse constante, mais que nous voulons accélérer à 1 m/s2. Ce nouveau problème présente deux changements importants - tout d'abord, nous n'avons plus à calculer la tension due à la gravité, parce que notre corde n'est pas de supporter le poids contre sa force. Deuxièmement, nous avons à rendre compte de la tension causée par la friction, ainsi que celle causée par l'accélération du poids de la masse. Nous arriverons à résoudre comme suit:
- la force Normale (N) = 10 kg × 9,8 (de l'accélération de la pesanteur) = 98 N
- la Force de frottement (Fr) = 0.5 × 98 N = 49 Newton
- la Force d'accélération (Fa) = 10 kg × 1 m/s2 = 10 Newtons
- Total tension = Fr Fa = 49 10 = 59 Newtons.
@@_
@@
Méthode 2
le Calcul des Tensions Sur Plusieurs Brins


1
@@_
@@Levage parallèle des charges verticales à l'aide d'une poulie. Les poulies sont des machines simples consistant en une suspension de disque qui permet à la force de tension dans un câble pour changer de direction. Dans une simple poulie de configuration, la corde ou le câble fonctionne à partir d'un poids suspendu jusqu'à la poulie, puis vers le bas à l'autre, la création de 2 longueurs de corde ou de câble à brins. Cependant, la tension dans les deux sections de la corde est égale, même si les deux extrémités de la corde sont tirés par les forces de différentes grandeurs. Pour un système de deux masses suspendues à partir d'une verticale de la poulie de tension est égale à 2g(m1)(m2)/(m2 m1), où 'g' est l'accélération de la pesanteur, m1 est la masse de l'objet 1, et 'm2' est la masse de l'objet 2.
- Note que, habituellement, les problèmes de physique assumer idéal poulies - sans masse, sans friction, poulies qui ne peut pas se casser, se déformer, ou sont séparées du plafond, de la corde, etc. qui les prend en charge.
- disons que nous avons deux poids suspendus à la verticale d'une poulie dans des axes parallèles. Poids 1, a une masse de 10 kg, poids 2 a une masse de 5 kg. Dans ce cas, nous trouvons la tension comme suit:
- T = 2g(m1)(m2)/(m2 m1)
- T = 2(9.8)(10)(5)/(5 10)
- T = 19.6(50)/(15)
- T = 980/15
- T = 65.33 Newtons.
- Notez que, en raison d'un poids plus lourd que les autres, toutes autres choses étant égales par ailleurs, ce système va commencer à s'accélérer, avec 10 kg en mouvement à la baisse et les 5 kg de poids se déplaçant vers le haut.
2
@@_
@@Soulever des charges à l'aide d'une poulie avec les non-parallèle des chaînes verticales. Les poulies sont souvent utilisés pour diriger la tension dans une direction autre que celle vers le haut ou vers le bas. Si, par exemple, un poids est suspendu verticalement à partir d'une extrémité de la corde tandis que l'autre extrémité est reliée à un deuxième poids sur une diagonale de la pente, de la non-parallèle un système de poulie prend la forme d'un triangle avec des points lors de la première de poids, la deuxième de poids, et la poulie. Dans ce cas, la tension dans la corde est affecté à la fois par la force de la gravité, le poids et par la composante de la force de traction qui est parallèle à la diagonale de la section de la corde.
- disons que nous avons un système avec 10 kg de poids (m1) suspendu verticalement reliés par une poulie pour 5 kg de poids (m2), une de 60 degrés de la rampe (à supposer que la rampe est de frottement).Pour trouver la tension dans la corde, il est plus facile de trouver des équations pour les forces de l'accélération du poids en premier. Procédez comme suit:
- La pendaison de poids est plus lourd et nous ne sommes pas traiter avec frottement, donc nous savons que cela permettra d'accélérer à la baisse. La tension dans la corde en tirant sur elle, cependant, de sorte que c'est l'accélération due à la force résultante F = m1(g) - T, ou 10(9.8) - T = 98 - T.
- Nous savons que le poids sur la rampe d'accélérer jusqu'à la rampe. Depuis la rampe est de friction, nous savons que la tension est à son tirant vers le haut de la rampe et que son propre poids est de tirer vers le bas. La composante de la force de traction vers le bas de la rampe est donné par le péché(?), ainsi, dans notre cas, on peut dire que c'est l'accélération de la rampe en raison de la force F = T - m2(g)sin(60) = T - 5(9.8)(.87) = T - 42.63.
- l'Accélération de la deux poids sont les mêmes, donc nous avons (98 - T)/m1 = (T - 42.63) /m2. Après un peu trivial de travail pour résoudre cette équation, nous avons enfin T = 60.96 Newton.
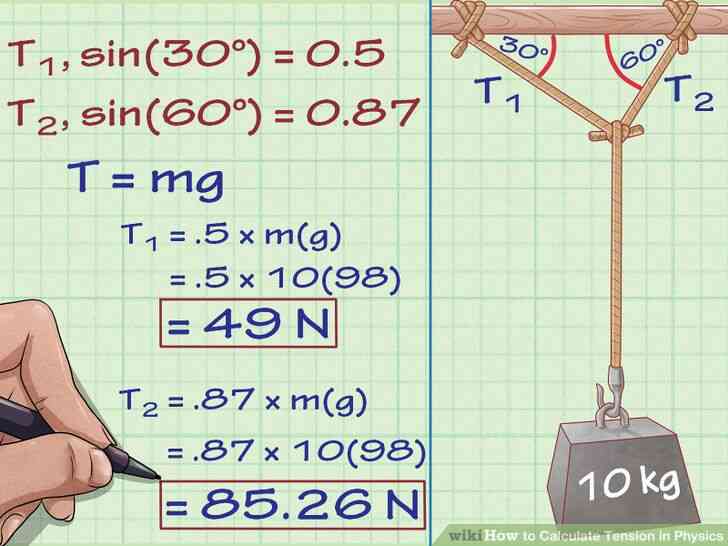
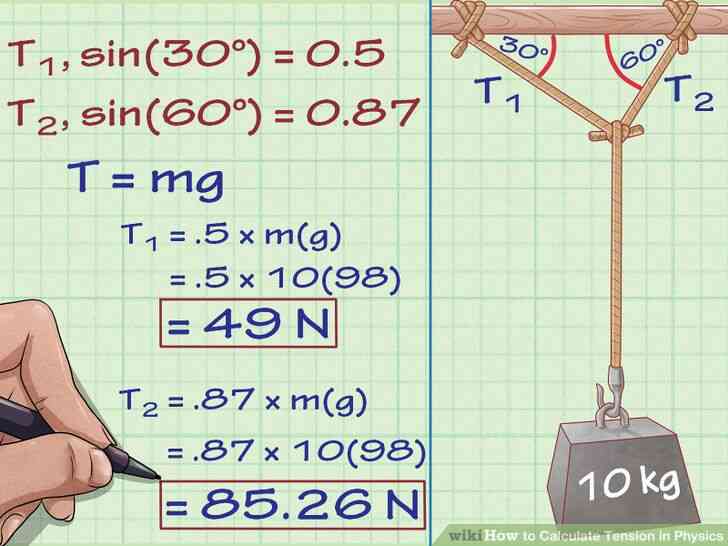
3
@@_
@@Utiliser plusieurs brins à l'appui d'une pendaison de l'objet. Enfin, considérons un objet suspendu à un 'Y-en forme de' système de cordes - deux cordes sont fixés au plafond, qui se rencontrent à un point central à partir duquel un poids se bloque par un troisième corde. La tension dans la troisième corde est évident - c'est tout simplement la tension résultant de la force gravitationnelle, ou de m(g). Les tensions dans les deux autres cordes sont différentes et doivent ajouter jusqu'à égaler la force de gravité vers le haut à la verticale et à l'égalité de zéro dans la direction horizontale, en supposant que le système est au repos. La tension dans la corde est affecté à la fois par la masse de la pendaison de poids et par l'angle sous lequel chaque corde se réunit au plafond.
- disons dans notre en forme de Y système de bas poids d'une masse de 10 kg et que les deux haut des cordes au plafond à 30 degrés et 60 degrés respectivement. Si nous voulons trouver la tension dans chaque de la partie supérieure des cordes, nous devons considérer chaque tension verticales et horizontales des composants. Néanmoins, dans cet exemple, les deux cordes se trouve être perpendiculaires les uns aux autres, rendant facile pour nous de calculer selon les définitions de fonctions trigonométriques comme suit:
- Le rapport entre T1 ou T2 et T = m(g) est égal au sinus de l'angle entre chaque appui de la corde et le plafond. Pour T1, sin(30) = 0.5, alors que pour les T2, sin(60) = 0.87
- Multiplier la tension dans le bas de la corde (T = mg) par le sinus de chaque angle de trouver de T1 et de T2.
- T1 = .5 × m(g) = .5 × 10(98) = 49 Newtons.
- T2 = .87 × m(g) = .87 × 10(98) = 85.26 Newtons.
Comment Calculer la Tension dans la Physique
En physique, la tension est la force exercee par une corde, une chaîne, un cable ou tout autre objet similaire sur un ou plusieurs objets. Rien retire, suspendu, prise en charge, ou en passant d'une corde, chaîne, cable, etc. est soumis a la force de tension. Comme toutes les forces, les tensions peuvent accelerer objets ou de provoquer une deformation. Etre capable de calculer la tension est une competence importante non seulement pour les etudiants en physique, mais aussi pour les ingenieurs et les architectes, qui, a construire des batiments sûrs, doit savoir si la tension sur une corde ou d'un cable peut resister a la deformation causee par le poids de l'objet avant de ceder et de se casser. Voir l'Etape 1 pour savoir comment calculer la tension dans plusieurs systemes physiques.
Mesures
@@_
@@
Methode 1
Determination de la Tension Sur un Seul Brin


1
@@_
@@Definir les forces sur l'une des extremites de la fibre. La tension dans un brin de ficelle ou de la corde est le resultat des forces de traction sur la corde de chaque extremite. Pour rappel, force = masse × acceleration. En supposant que la corde est tendue, tout changement de l'acceleration ou de masse dans les objets de la corde soutient va provoquer un changement dans la tension dans la corde. Ne pas oublier la constante d'acceleration due a la gravite (meme si un systeme est au repos, ses composants sont soumis a cette force. Nous pouvons penser a une tension dans la corde que T = (m × g) (m × a), ou 'g' est l'acceleration due a la gravite de tous les objets de la corde est de soutenir et de 'une' est tout autre acceleration sur tous les objets de la corde soutient.
- Pour les besoins de la plupart des problemes de physique, nous supposons ideal cordes - en d'autres termes, que notre corde, cable, etc. est mince, de masse nulle, et ne peut pas etre etire ou casse.
- Comme un exemple, considerons un systeme ou un poids suspendu a une poutre de bois par l'intermediaire d'un seul cable (voir photo). Ni le poids ni la corde sont en mouvement l'ensemble du systeme est au repos. De ce fait, nous savons que, pour le poids d'etre tenue dans l'equilibre, la force de tension doit etre egale a la force de gravite sur le poids. En d'autres termes, la Tension (Ft) = Force de gravite (Fg) = m × g.
- en Supposant une 10 kg de poids, alors, la force de tension est de 10 kg × 9,8 m/s2 = 98 Newtons.


2
@@_
@@Compte pour l'acceleration. La gravite n'est pas la seule force qui peut affecter la tension d'une corde - alors, peut-toute la force liee a l'acceleration d'un objet, la corde est attachee. Si, par exemple, une suspension de l'objet est accelere par une force sur la corde ou le cable, la force d'acceleration (masse × acceleration) est ajoutee a la tension provoquee par le poids de l'objet.
- disons que, dans notre exemple de l'10 kg de poids suspendu par une corde, qui, au lieu d'etre fixe a une poutre de bois, la corde est effectivement utilise pour tirer le poids vers le haut a une acceleration de 1 m/s2. Dans ce cas, nous devons tenir compte de l'acceleration sur le poids ainsi que la force de gravite par la resolution comme suit:
- Pi = Fg m × a
- Pi = 98 10 kg × 1 m/s2
- Pi = 108 Newtons.


3
@@_
@@Compte pour l'acceleration de rotation. Un objet en rotation autour d'un point central au moyen d'une corde (comme un pendule) exerce une pression sur la corde causee par la force centripete. La force centripete est ajoutee force de tension de la corde exerce en 'tirant' vers l'interieur pour garder un objet en mouvement dans l'arc et non pas en ligne droite. Plus l'objet est en mouvement, plus grande est la force centripete. La force centripete (Fc) est egal a m × v2/r, ou 'm' est la masse, le 'v' est la vitesse, et 'r' est le rayon du cercle qui contient l'arc de mouvement de l'objet.
- Depuis la direction et l'amplitude de la force centripete changements que l'objet sur la corde, les deplacements et les changements de vitesses, de sorte que le total de la tension dans la corde, qui tire toujours parallele a la corde vers le point central. Rappelez-vous aussi que la force de gravite est constamment en agissant sur l'objet dans une direction vers le bas. Donc, si un objet est en train de provoquer ou bascule a la verticale, le total de la tension est au plus bas de l'arc (pour un pendule, ce qui est appele le point d'equilibre) lorsque l'objet est en mouvement plus rapide et la moins au sommet de l'arc lorsqu'il est en mouvement plus lent.
- disons que dans notre exemple, le probleme que notre objet n'est plus l'acceleration de la hausse, mais au lieu de se balancer comme un pendule. On va dire que notre corde de 1,5 m (4,9 pi) de long et que notre poids se deplace a 2 m/s lorsqu'il passe a travers le fond de son swing. Si nous voulons calculer la tension a la partie inferieure de l'arc lorsqu'il est plus haut, il faudrait d'abord reconnaître que la tension due a la gravite, a ce point est le meme que lorsque le poids etait tenu immobile - 98 Newtons.Afin de trouver le supplement de la force centripete, nous permettrait de resoudre comme suit:
- Fc = m × v2/r
- Fc = 10 × 22/1.5
- Fc =10 × 2.67 = 26.7 Newtons.
- Donc, notre le total de la tension serait de 98 a 26,7 = 124.7 Newtons.


4
@@_
@@Comprendre que la tension due a la gravite des changements tout au long d'un balancement de l'objet a l'arc. Comme indique ci-dessus, a la fois la direction et l'amplitude de la force centripete le changement comme un objet de balançoires. Cependant, bien que la force de gravite qui reste constant, la tension qui resulte de la gravite change egalement. Quand le swing d'un objet n'est pas au fond de son arc (son point d'equilibre), la gravite est en tirant directement vers le bas, mais la tension est de tirer vers le haut a un angle. De ce fait, la tension n'a qu'a neutraliser une partie de la force due a la gravite, plutot que de son integralite.
- Rupture de la force gravitationnelle entre deux vecteurs peuvent vous aider a visualiser ce concept. A un moment donne dans l'arc de la verticale a balancer de l'objet, de la corde forme un angle '?', avec la ligne passant par le point d'equilibre et le point central de rotation. Comme le pendule, la force gravitationnelle (m × g) peut etre decompose en deux vecteurs - mgsin(?) en agissant de la tangente a l'arc dans la direction du point d'equilibre et mgcos(?) agissant en parallele a la force de tension dans la direction opposee. La Tension n'a qu'a contre mgcos(?) - la force qui attire contre elle - et non l'ensemble de la force gravitationnelle (sauf au point d'equilibre, lorsque ceux-ci sont egaux).
- disons que lorsque notre pendule forme un angle de 15 degres avec la verticale, il se deplace a 1,5 m/s. Nous trouverions de la tension par la resolution comme suit:
- Tension due a la gravite (Tg) = 98cos(15) = 98(0.96) = 94.08 Newton
- la force Centripete (Fc) = 10 × 1.52/1.5 = 10 × 1.5 = 15 Newton
- Total tension = Tg Fc = 94.08 15 = 109.08 Newtons.


5
@@_
@@Compte pour le frottement. Tout objet tire par une corde que l'experience d'un 'glisser' de la force de friction contre un autre objet (ou fluide) les transferts de cette force de la tension dans la corde. La Force de frottement entre les deux objets est calcule comme dans toute autre situation - par l'equation suivante: Force due a la friction (generalement ecrites Fr) = (mu)N, ou mu est le coefficient de frottement entre les deux objets et N est la normale a la force entre les deux objets, ou la force avec laquelle ils sont en appuyant les uns les autres. Notez que le frottement statique - la friction que les resultats lorsque vous essayez de mettre un objet a l'arret en mouvement est different de celui de frottement le frottement que les resultats en essayant de garder un objet en mouvement en mouvement.
- disons que l'une de nos 10 kg de poids n'est plus balance, mais est maintenant deplacee horizontalement sur le sol par notre corde. Disons que le sol a un coefficient de frottement cinetique entre 0,5 et que notre poids se deplace a une vitesse constante, mais que nous voulons accelerer a 1 m/s2. Ce nouveau probleme presente deux changements importants - tout d'abord, nous n'avons plus a calculer la tension due a la gravite, parce que notre corde n'est pas de supporter le poids contre sa force. Deuxiemement, nous avons a rendre compte de la tension causee par la friction, ainsi que celle causee par l'acceleration du poids de la masse. Nous arriverons a resoudre comme suit:
- la force Normale (N) = 10 kg × 9,8 (de l'acceleration de la pesanteur) = 98 N
- la Force de frottement (Fr) = 0.5 × 98 N = 49 Newton
- la Force d'acceleration (Fa) = 10 kg × 1 m/s2 = 10 Newtons
- Total tension = Fr Fa = 49 10 = 59 Newtons.
@@_
@@
Methode 2
le Calcul des Tensions Sur Plusieurs Brins


1
@@_
@@Levage parallele des charges verticales a l'aide d'une poulie. Les poulies sont des machines simples consistant en une suspension de disque qui permet a la force de tension dans un cable pour changer de direction. Dans une simple poulie de configuration, la corde ou le cable fonctionne a partir d'un poids suspendu jusqu'a la poulie, puis vers le bas a l'autre, la creation de 2 longueurs de corde ou de cable a brins. Cependant, la tension dans les deux sections de la corde est egale, meme si les deux extremites de la corde sont tires par les forces de differentes grandeurs. Pour un systeme de deux masses suspendues a partir d'une verticale de la poulie de tension est egale a 2g(m1)(m2)/(m2 m1), ou 'g' est l'acceleration de la pesanteur, m1 est la masse de l'objet 1, et 'm2' est la masse de l'objet 2.
- Note que, habituellement, les problemes de physique assumer ideal poulies - sans masse, sans friction, poulies qui ne peut pas se casser, se deformer, ou sont separees du plafond, de la corde, etc. qui les prend en charge.
- disons que nous avons deux poids suspendus a la verticale d'une poulie dans des axes paralleles. Poids 1, a une masse de 10 kg, poids 2 a une masse de 5 kg. Dans ce cas, nous trouvons la tension comme suit:
- T = 2g(m1)(m2)/(m2 m1)
- T = 2(9.8)(10)(5)/(5 10)
- T = 19.6(50)/(15)
- T = 980/15
- T = 65.33 Newtons.
- Notez que, en raison d'un poids plus lourd que les autres, toutes autres choses etant egales par ailleurs, ce systeme va commencer a s'accelerer, avec 10 kg en mouvement a la baisse et les 5 kg de poids se deplaçant vers le haut.
2
@@_
@@Soulever des charges a l'aide d'une poulie avec les non-parallele des chaînes verticales. Les poulies sont souvent utilises pour diriger la tension dans une direction autre que celle vers le haut ou vers le bas. Si, par exemple, un poids est suspendu verticalement a partir d'une extremite de la corde tandis que l'autre extremite est reliee a un deuxieme poids sur une diagonale de la pente, de la non-parallele un systeme de poulie prend la forme d'un triangle avec des points lors de la premiere de poids, la deuxieme de poids, et la poulie. Dans ce cas, la tension dans la corde est affecte a la fois par la force de la gravite, le poids et par la composante de la force de traction qui est parallele a la diagonale de la section de la corde.
- disons que nous avons un systeme avec 10 kg de poids (m1) suspendu verticalement relies par une poulie pour 5 kg de poids (m2), une de 60 degres de la rampe (a supposer que la rampe est de frottement).Pour trouver la tension dans la corde, il est plus facile de trouver des equations pour les forces de l'acceleration du poids en premier. Procedez comme suit:
- La pendaison de poids est plus lourd et nous ne sommes pas traiter avec frottement, donc nous savons que cela permettra d'accelerer a la baisse. La tension dans la corde en tirant sur elle, cependant, de sorte que c'est l'acceleration due a la force resultante F = m1(g) - T, ou 10(9.8) - T = 98 - T.
- Nous savons que le poids sur la rampe d'accelerer jusqu'a la rampe. Depuis la rampe est de friction, nous savons que la tension est a son tirant vers le haut de la rampe et que son propre poids est de tirer vers le bas. La composante de la force de traction vers le bas de la rampe est donne par le peche(?), ainsi, dans notre cas, on peut dire que c'est l'acceleration de la rampe en raison de la force F = T - m2(g)sin(60) = T - 5(9.8)(.87) = T - 42.63.
- l'Acceleration de la deux poids sont les memes, donc nous avons (98 - T)/m1 = (T - 42.63) /m2. Apres un peu trivial de travail pour resoudre cette equation, nous avons enfin T = 60.96 Newton.
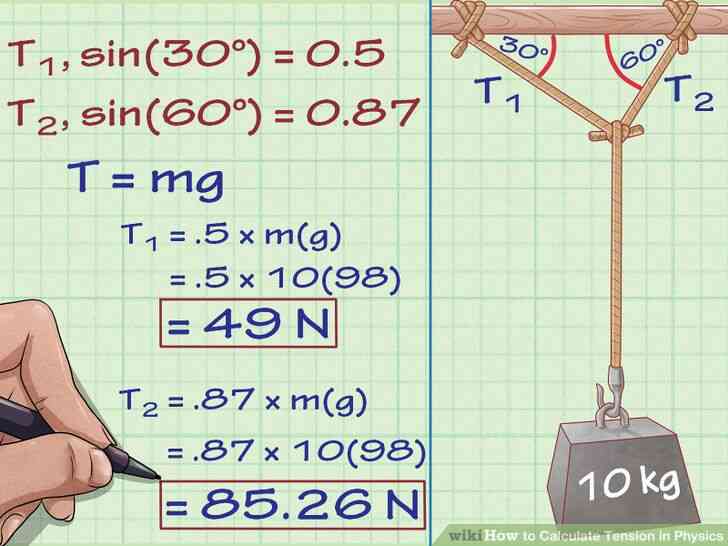
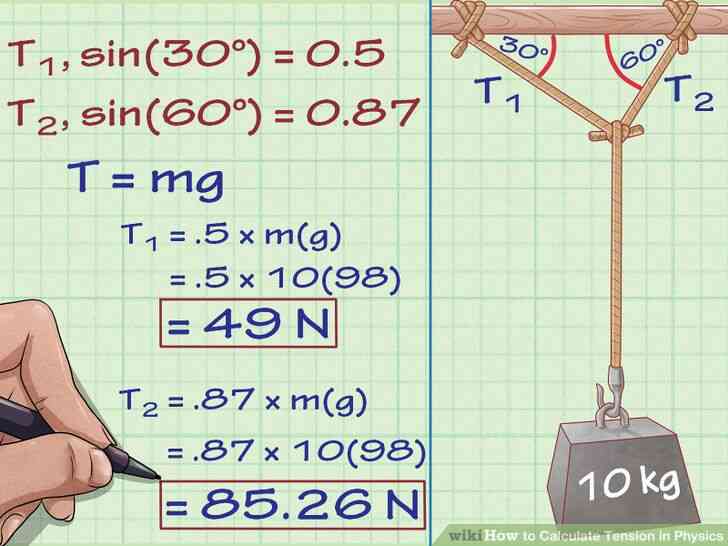
3
@@_
@@Utiliser plusieurs brins a l'appui d'une pendaison de l'objet. Enfin, considerons un objet suspendu a un 'Y-en forme de' systeme de cordes - deux cordes sont fixes au plafond, qui se rencontrent a un point central a partir duquel un poids se bloque par un troisieme corde. La tension dans la troisieme corde est evident - c'est tout simplement la tension resultant de la force gravitationnelle, ou de m(g). Les tensions dans les deux autres cordes sont differentes et doivent ajouter jusqu'a egaler la force de gravite vers le haut a la verticale et a l'egalite de zero dans la direction horizontale, en supposant que le systeme est au repos. La tension dans la corde est affecte a la fois par la masse de la pendaison de poids et par l'angle sous lequel chaque corde se reunit au plafond.
- disons dans notre en forme de Y systeme de bas poids d'une masse de 10 kg et que les deux haut des cordes au plafond a 30 degres et 60 degres respectivement. Si nous voulons trouver la tension dans chaque de la partie superieure des cordes, nous devons considerer chaque tension verticales et horizontales des composants. Neanmoins, dans cet exemple, les deux cordes se trouve etre perpendiculaires les uns aux autres, rendant facile pour nous de calculer selon les definitions de fonctions trigonometriques comme suit:
- Le rapport entre T1 ou T2 et T = m(g) est egal au sinus de l'angle entre chaque appui de la corde et le plafond. Pour T1, sin(30) = 0.5, alors que pour les T2, sin(60) = 0.87
- Multiplier la tension dans le bas de la corde (T = mg) par le sinus de chaque angle de trouver de T1 et de T2.
- T1 = .5 × m(g) = .5 × 10(98) = 49 Newtons.
- T2 = .87 × m(g) = .87 × 10(98) = 85.26 Newtons.
Comment Calculer la Tension dans la Physique
By commentfaire
En physique, la tension est la force exercée par une corde, une chaîne, un câble ou tout autre objet similaire sur un ou plusieurs objets. Rien retiré, suspendu, prise en charge, ou en passant d'une corde, chaîne, câble, etc. est soumis à la force de tension. Comme toutes les forces, les tensions peuvent accélérer objets ou de provoquer une déformation. Être capable de calculer la tension est une compétence importante non seulement pour les étudiants en physique, mais aussi pour les ingénieurs et les architectes, qui, à construire des bâtiments sûrs, doit savoir si la tension sur une corde ou d'un câble peut résister à la déformation causée par le poids de l'objet avant de céder et de se casser. Voir l'Étape 1 pour savoir comment calculer la tension dans plusieurs systèmes physiques.