Vous pouvez ajouter une série de nombres impairs consécutifs à la main, mais il y a un moyen beaucoup plus facile de le faire, surtout si vous avez affaire à un beaucoup de chiffres. Une fois que vous maîtrisez une formule simple, vous serez en mesure d'ajouter ces numéros en un rien de temps, sans utiliser de calculatrice. Il est également un moyen simple pour savoir lequel des nombres consécutifs ajouter jusqu'à une somme donnée.
Mesures
@@_
@@
Partie 1
en Appliquant la Formule pour l'Ajout d'une Séquence de Nombres Impairs Consécutifs


1
@@_
@@Choisir un point de fin. Avant de commencer, vous devez déterminer quel est le dernier numéro consécutif dans votre jeu. Cette formule peut vous aider à ajouter un nombre quelconque de nombres impairs consécutifs, en commençant par 1.[1]
- Si vous travaillez sur un projet, ce numéro vous sera attribué. Par exemple, si la question vous demande de trouver la somme de tous les nombres impairs consécutifs entre 1 et 81, votre point d'arrivée est de 81.
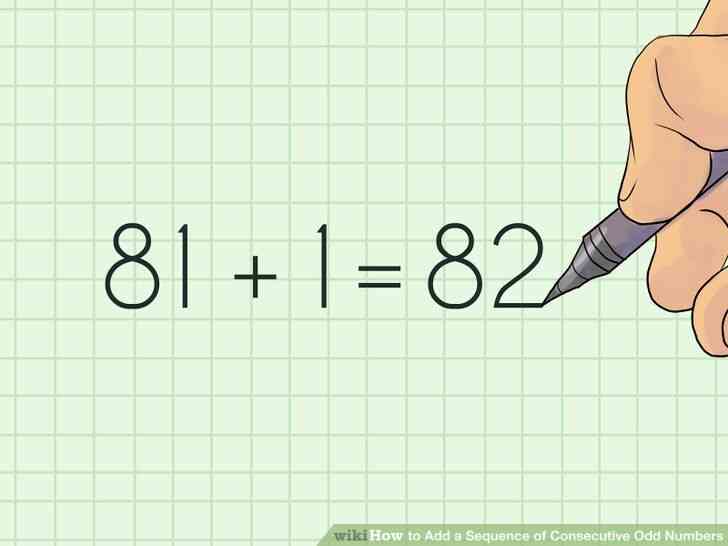
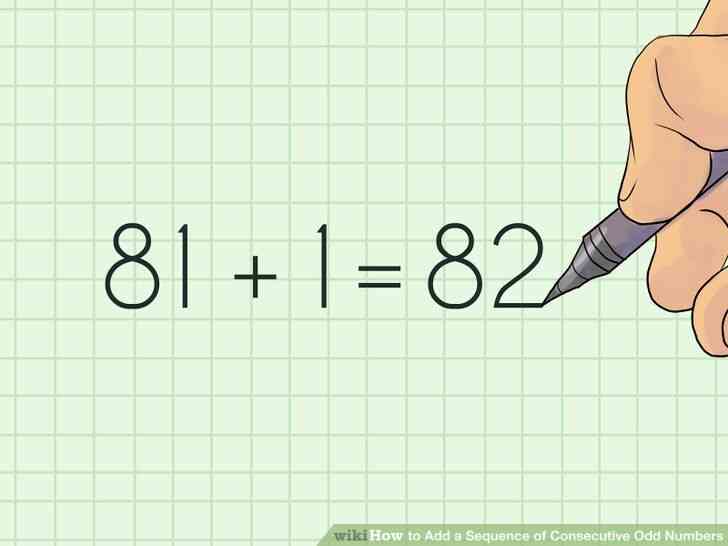
2
@@_
@@Ajouter 1. La prochaine étape est de simplement ajouter 1 pour votre point de fin. Vous devriez maintenant avoir un nombre pair, ce qui est essentiel pour l'étape suivante.
- Par exemple, si votre point d'arrivée est 81, 81 1 = 82.
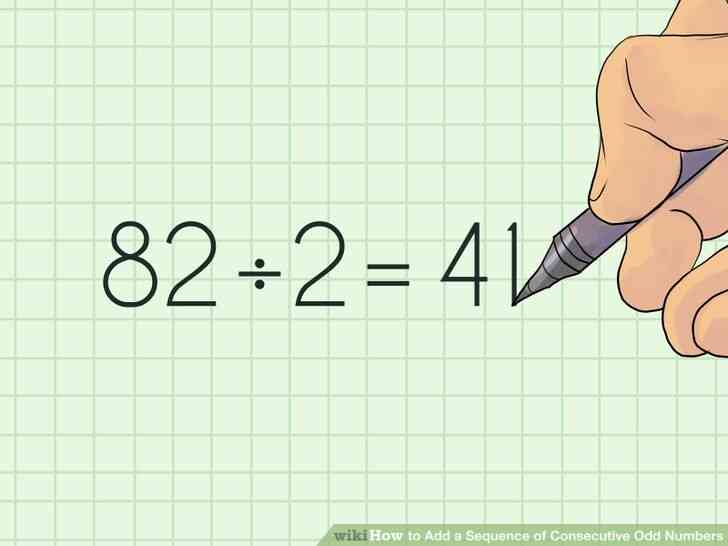
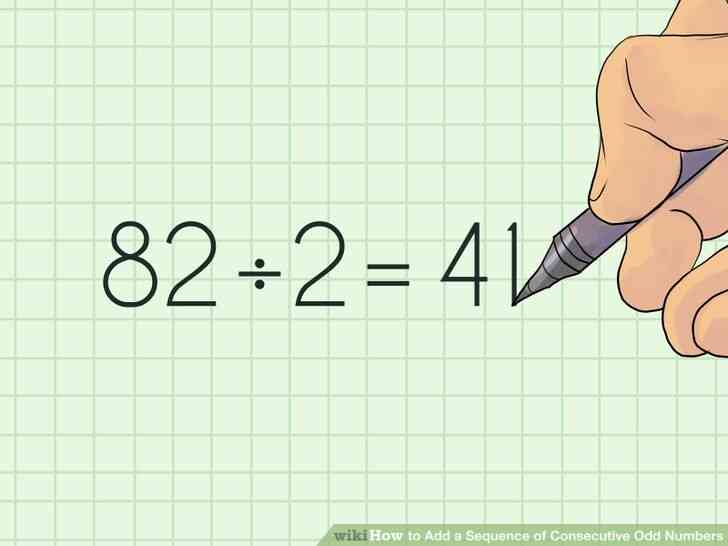
3
@@_
@@Diviser par 2. Une fois que vous avez un nombre pair, vous devriez diviser ce résultat par 2. Cela vous donnera un nombre impair est égal au nombre de chiffres qui sont ajoutés ensemble.
- Par exemple, 82 / 2 = 41.
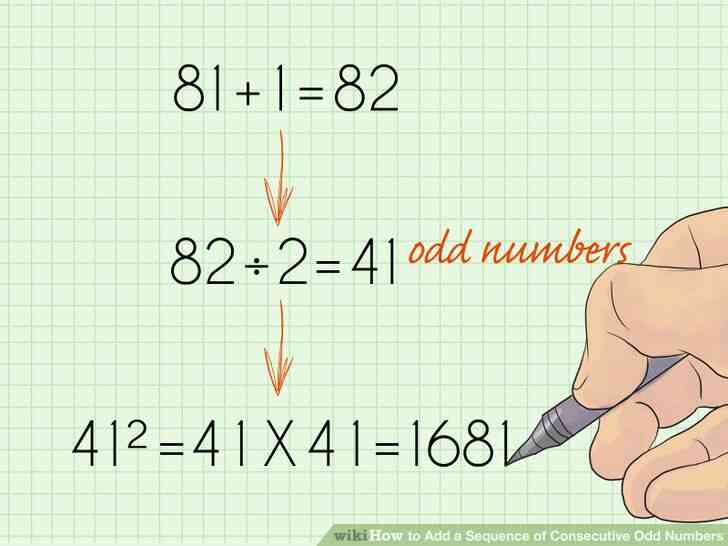
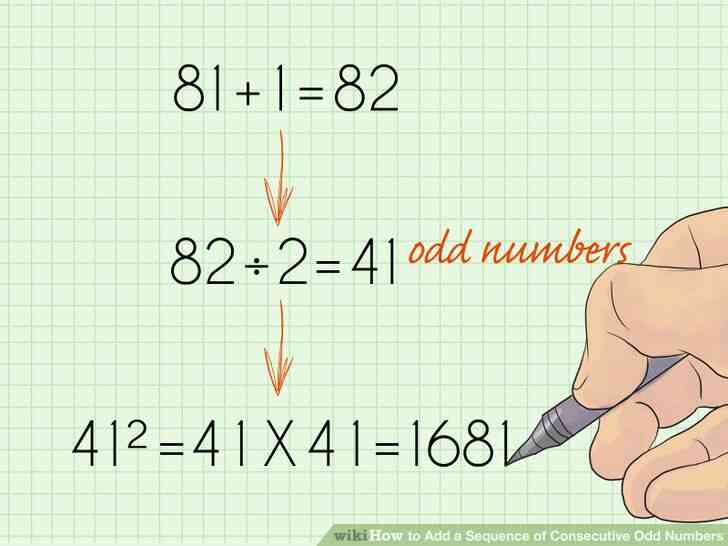
4
@@_
@@Carré de la somme. La dernière étape consiste à carré le nombre, ou de le multiplier par lui-même. Une fois que vous faites cela, vous aurez votre réponse.
- Par exemple, 41 x 41 = 1681. Cela signifie que la somme de tous les nombres impairs consécutifs entre 1 et 81 est 1681.
@@_
@@
Partie 2
Comprendre Pourquoi la Formule Fonctionne
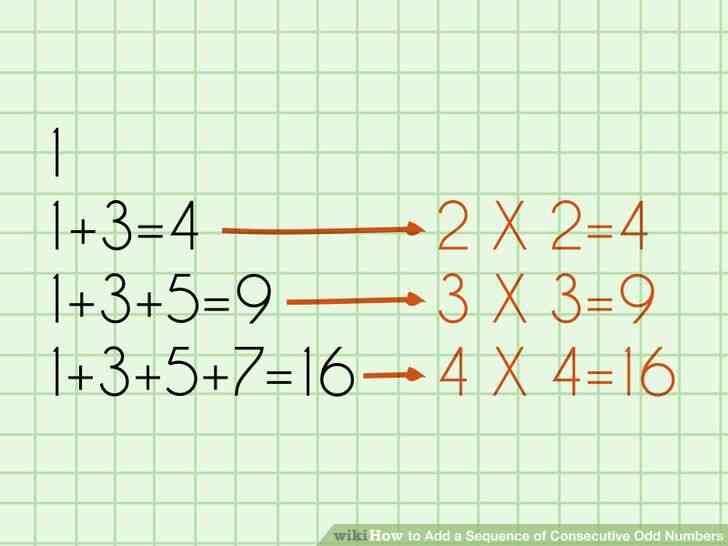
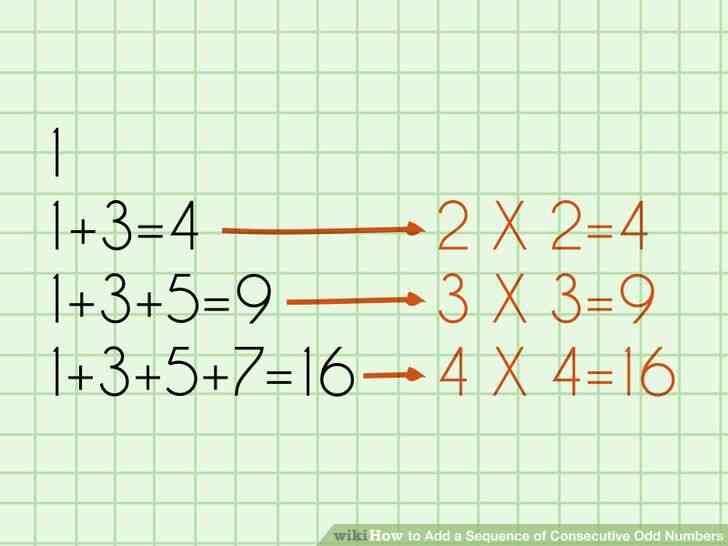
1
@@_
@@Observer le motif. La clé de la compréhension de cette formule est de reconnaître que le modèle sous-jacent. La somme de tout ensemble de nombres impairs consécutifs à partir de 1 est toujours égal au carré du nombre de chiffres qui ont été ajoutés ensemble.
- Somme du premier nombre impair = 1
- Somme des deux premiers nombres impairs = 1 3 = 4 (= 2 x 2).
- Somme des trois premiers nombres impairs = 1 3 5 = 9 (= 3 x 3).
- Somme des quatre premiers nombres impairs = 1 3 5 7 = 16 (= 4 x 4).
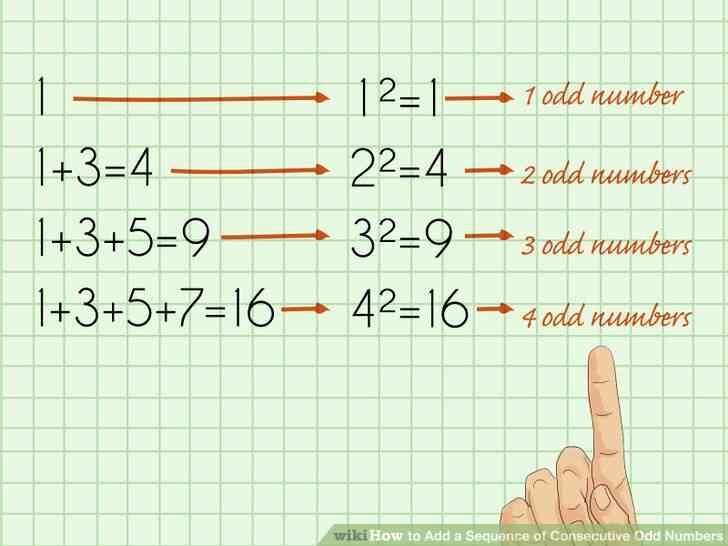
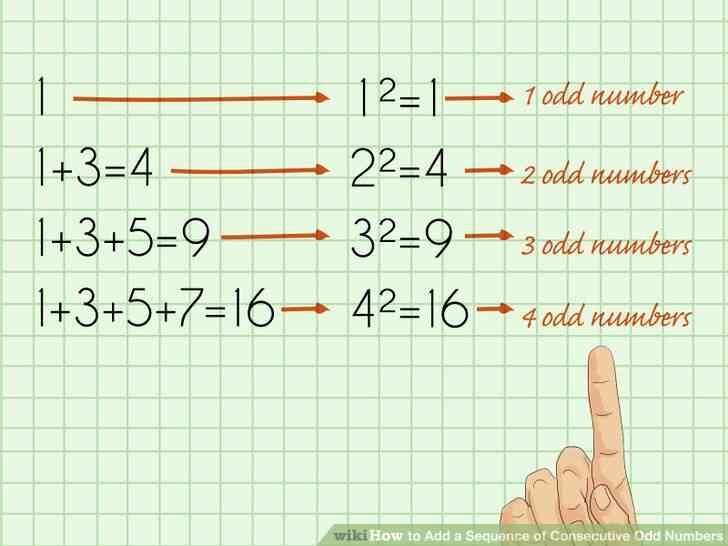
2
@@_
@@Comprendre les données provisoires. En résolvant ce problème, vous avez appris de plus que la somme des nombres. Vous avez également appris beaucoup de chiffres consécutifs ont été ajoutés: 41! C'est parce que le nombre de chiffres additionnés est toujours égale à la racine carrée de la somme.
- Somme du premier nombre impair = 1. La racine carrée de 1 est 1, et un seul chiffre a été ajouté.
- Somme des deux premiers nombres impairs = 1 3 = 4. La racine carrée de 4 est 2, et les deux chiffres ont été ajoutés.
- Somme des trois premiers nombres impairs = 1 3 5 = 9. La racine carrée de 9 est 3, et les trois chiffres ont été ajoutés.
- Somme des quatre premiers nombres impairs = 1 3 5 7 = 16. La racine carrée de 16 est 4, et quatre chiffres ont été ajoutés.
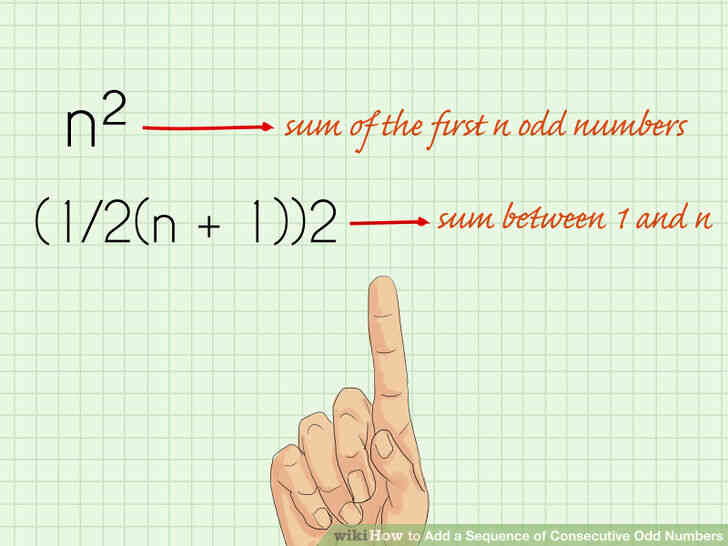
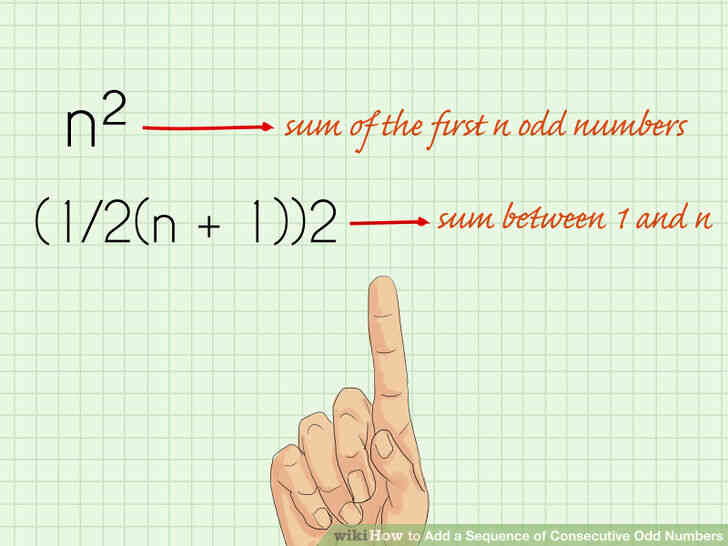
3
@@_
@@Généraliser la formule. Une fois que vous comprenez la formule et comment il fonctionne, vous pouvez l'écrire dans un format qui leur sera applicable n'importe quel nombre vous avez à faire. La formule pour trouver la somme des n premiers nombres impairs est n x n ou n au carré.
- Par exemple, si vous avez branché 41 pour n, vous auriez 41 x 41 ou 1681, qui est égal à la somme des 41 premiers nombres impairs.
- Si vous ne savez pas combien de numéros vous sont traiter avec, la formule pour déterminer la somme entre 1 et n (1/2(n 1))2
@@_
@@
Partie 3
Déterminer les Nombres Impairs Consécutifs Ajouter Jusqu'à un Montant


1
@@_
@@Comprendre la différence entre les deux types de problèmes. Si vous êtes donné une série de nombres impairs consécutifs et sont invités à trouver leur somme, vous devez utiliser l' (1/2(n 1))2 équation. Si, d'autre part, vous avez reçu une somme et a demandé de trouver la série des nombres impairs consécutifs qui ajoute à cette somme, vous aurez besoin d'utiliser une formule différente tous ensemble.


2
@@_
@@Laissez-n représente le premier numéro. Pour trouver ce que les nombres impairs consécutifs ajouter jusqu'à une somme donnée, vous devrez créer une formule algébrique. Commencez par utiliser n pour représenter le premier numéro de la séquence.[2]


3
@@_
@@Écrire les nombres restants en termes de n. Ensuite, vous devez déterminer comment écrire le reste des numéros dans l'ordre en termes de n. Parce qu'ils sont tous les nombres impairs consécutifs, il y aura une différence de deux entre chaque numéro.
- Cela signifie que le deuxième numéro de la série n 2, la troisième sera la n 4, etc.


4
@@_
@@Compléter votre formule. Une fois que vous savez comment représenter chaque nombre dans la série, il est temps d'écrire votre formule. Le côté gauche de votre formule devrait représenter les nombres de la série, et le côté droit devrait représenter leur somme.
- Par exemple, si vous avez été invité à trouver une série consécutive de deux nombres impairs que d'ajouter jusqu'à 128, on peut écrire n n 2 = 128.
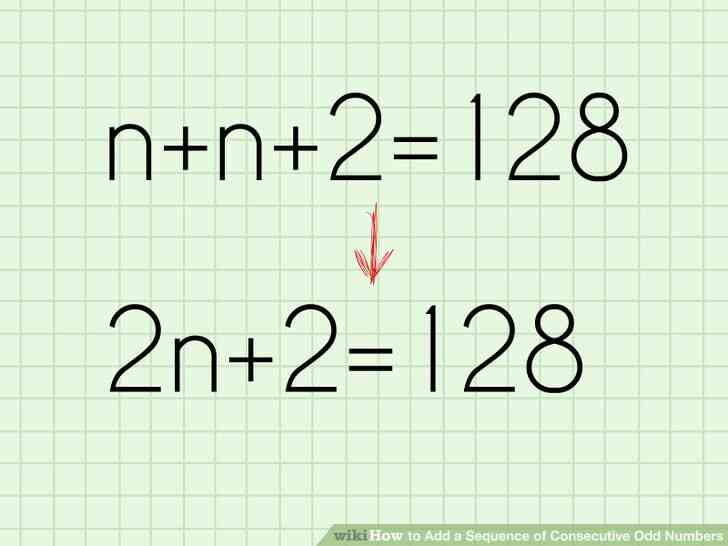
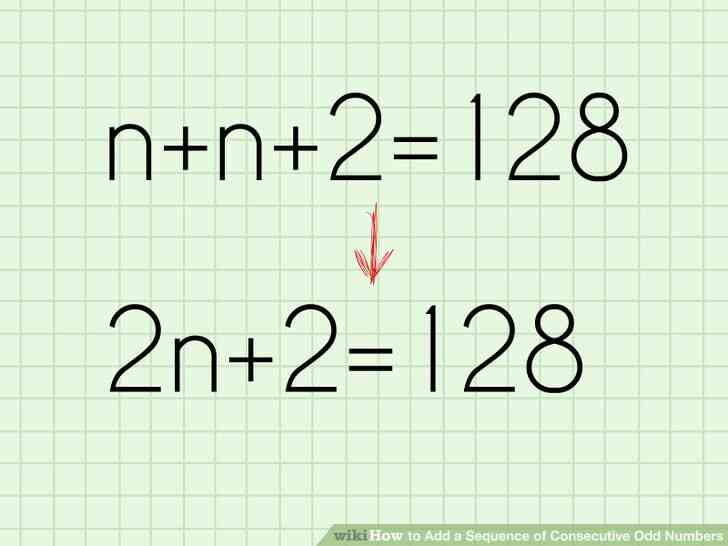
5
@@_
@@Simplifier l'équation. Si vous avez plus d'un n sur le côté gauche de l'équation, ajoutez-les ensemble. Ainsi, il sera beaucoup plus facile à résoudre.
- Par exemple, n n 2 = 128 simplifie à 2n 2 = 128.


6
@@_
@@Isoler n. La dernière étape de la résolution de cette équation est d'obtenir n, par lui-même sur un côté de l'équation. Rappelez-vous que toutes les modifications que vous apportez à un côté de l'équation, vous devez vous rendre de l'autre côté.
- Traiter avec l'addition et la soustraction de la première. Dans ce cas, vous devez soustraire 2 des deux côtés de l'équation pour obtenir n par lui-même , donc 2n = 126.
- Ensuite traiter avec la multiplication et la division. Dans ce cas, vous avez besoin de diviser les deux côtés par 2 afin d'isoler n, donc n = 113.
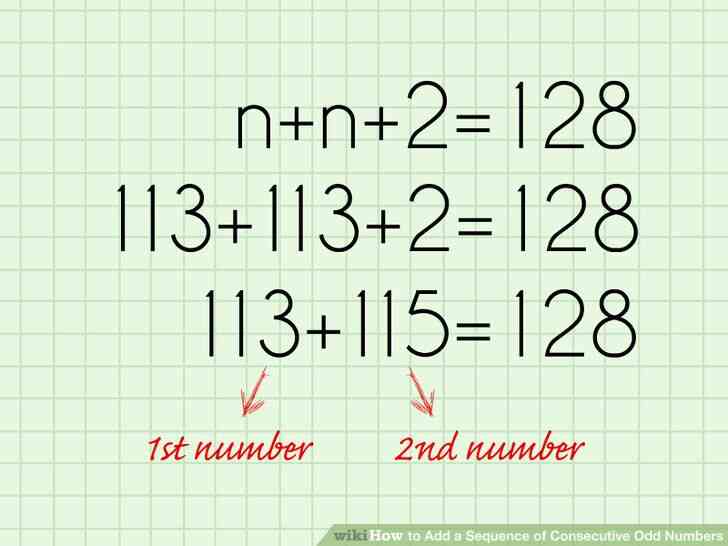
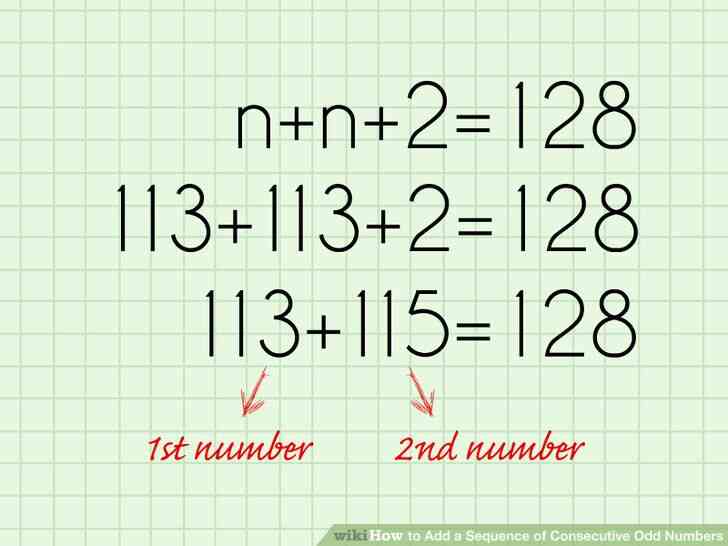
7
@@_
@@Écrire votre réponse. À ce stade, vous savez que n = 113, mais vous n'êtes pas tout à fait fini. Vous devez assurez-vous de répondre entièrement à la question qui a été posée. Si la question vous demande ce que la série de numéros consécutifs ajoute à une somme donnée, vous devez écrire tous les nombres.
- La réponse à ce problème est de 113 et 115 parce que n = 113 et n 2 = 115.
- C'est toujours une bonne idée de vérifier votre travail en branchant vos numéros de retour dans l'équation. Si ils ne sont pas égaux à la somme donnée, revenir en arrière et essayer à nouveau.
Comment Ajouter une Sequence de Nombres Impairs Consecutifs
Vous pouvez ajouter une serie de nombres impairs consecutifs a la main, mais il y a un moyen beaucoup plus facile de le faire, surtout si vous avez affaire a un beaucoup de chiffres. Une fois que vous maîtrisez une formule simple, vous serez en mesure d'ajouter ces numeros en un rien de temps, sans utiliser de calculatrice. Il est egalement un moyen simple pour savoir lequel des nombres consecutifs ajouter jusqu'a une somme donnee.
Mesures
@@_
@@
Partie 1
en Appliquant la Formule pour l'Ajout d'une Sequence de Nombres Impairs Consecutifs


1
@@_
@@Choisir un point de fin. Avant de commencer, vous devez determiner quel est le dernier numero consecutif dans votre jeu. Cette formule peut vous aider a ajouter un nombre quelconque de nombres impairs consecutifs, en commençant par 1.[1]
- Si vous travaillez sur un projet, ce numero vous sera attribue. Par exemple, si la question vous demande de trouver la somme de tous les nombres impairs consecutifs entre 1 et 81, votre point d'arrivee est de 81.
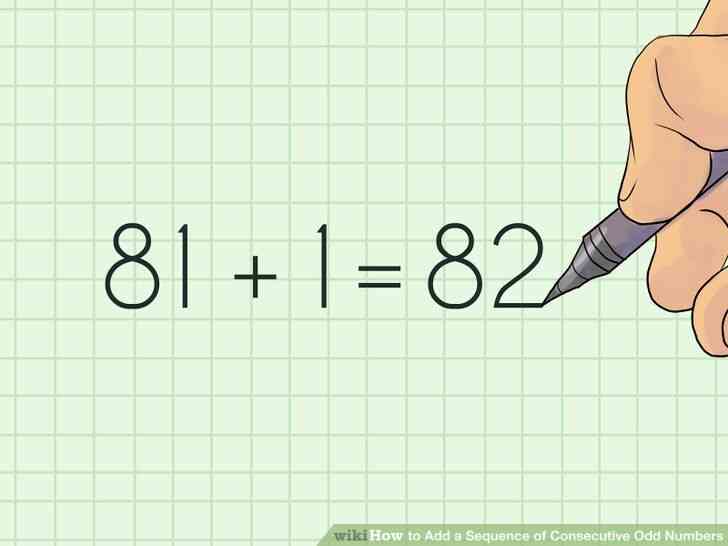
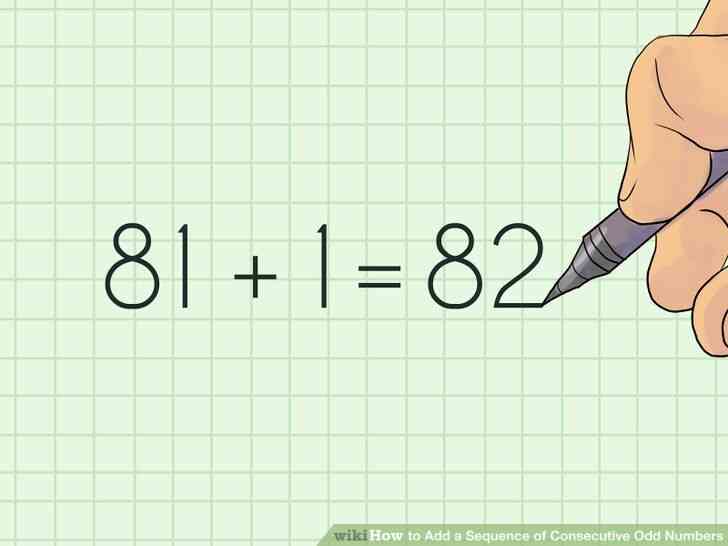
2
@@_
@@Ajouter 1. La prochaine etape est de simplement ajouter 1 pour votre point de fin. Vous devriez maintenant avoir un nombre pair, ce qui est essentiel pour l'etape suivante.
- Par exemple, si votre point d'arrivee est 81, 81 1 = 82.
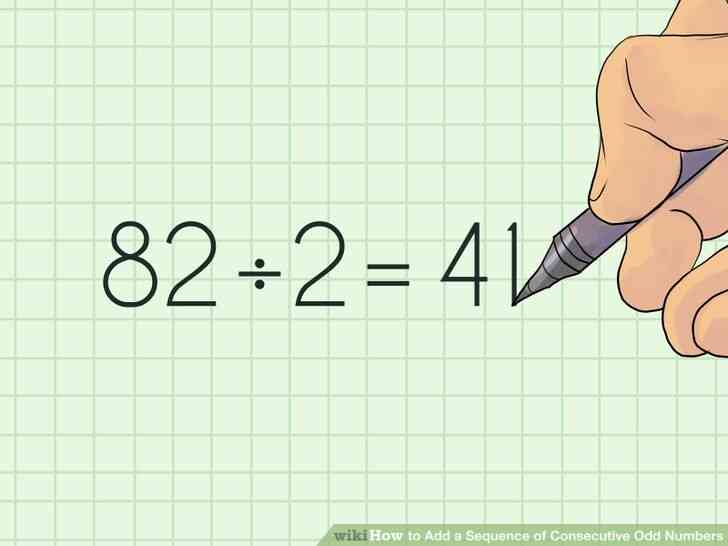
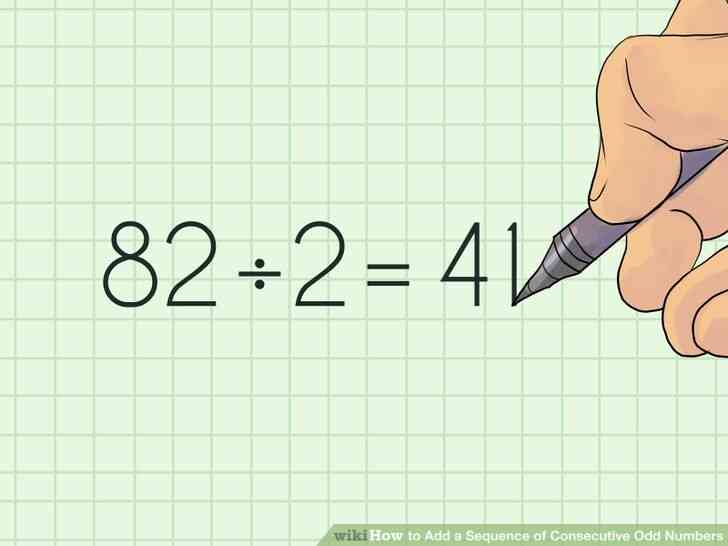
3
@@_
@@Diviser par 2. Une fois que vous avez un nombre pair, vous devriez diviser ce resultat par 2. Cela vous donnera un nombre impair est egal au nombre de chiffres qui sont ajoutes ensemble.
- Par exemple, 82 / 2 = 41.
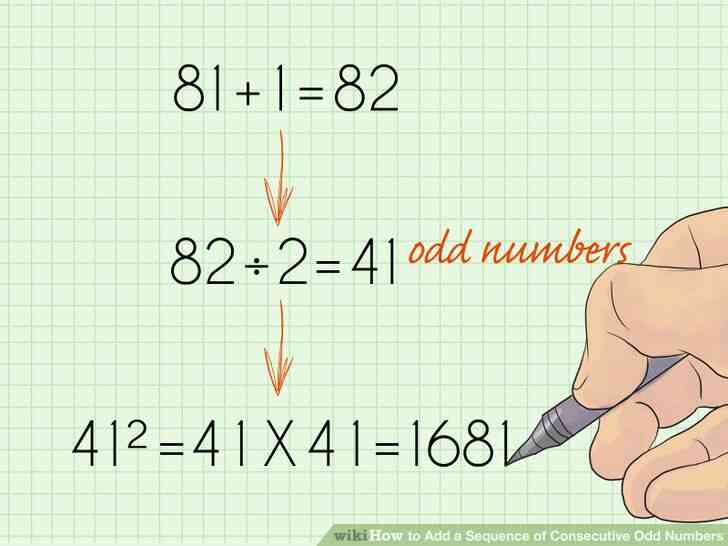
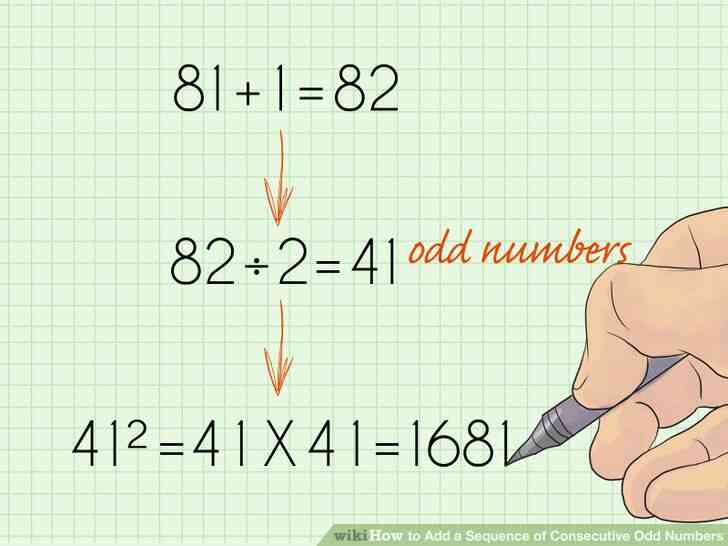
4
@@_
@@Carre de la somme. La derniere etape consiste a carre le nombre, ou de le multiplier par lui-meme. Une fois que vous faites cela, vous aurez votre reponse.
- Par exemple, 41 x 41 = 1681. Cela signifie que la somme de tous les nombres impairs consecutifs entre 1 et 81 est 1681.
@@_
@@
Partie 2
Comprendre Pourquoi la Formule Fonctionne
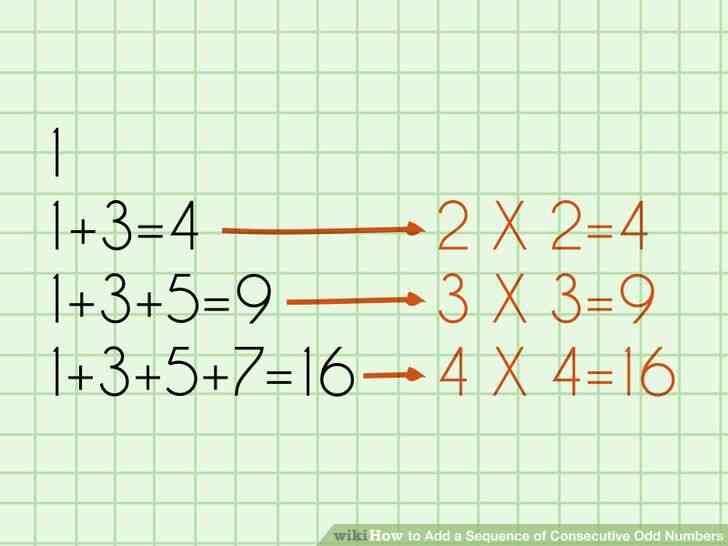
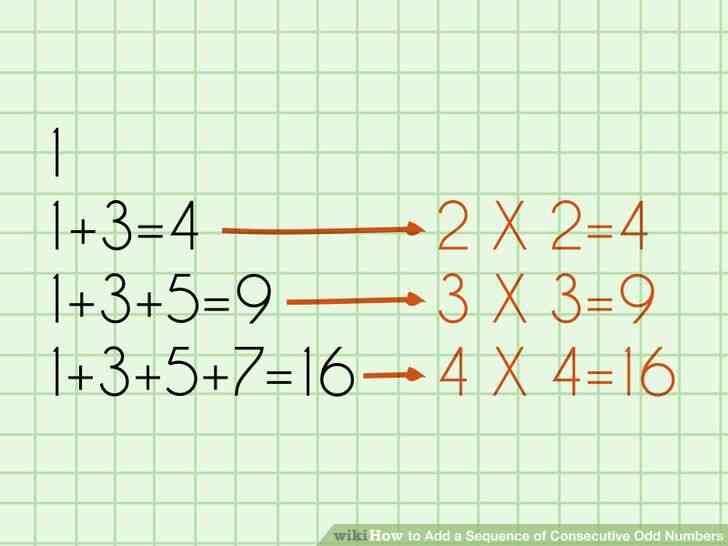
1
@@_
@@Observer le motif. La cle de la comprehension de cette formule est de reconnaître que le modele sous-jacent. La somme de tout ensemble de nombres impairs consecutifs a partir de 1 est toujours egal au carre du nombre de chiffres qui ont ete ajoutes ensemble.
- Somme du premier nombre impair = 1
- Somme des deux premiers nombres impairs = 1 3 = 4 (= 2 x 2).
- Somme des trois premiers nombres impairs = 1 3 5 = 9 (= 3 x 3).
- Somme des quatre premiers nombres impairs = 1 3 5 7 = 16 (= 4 x 4).
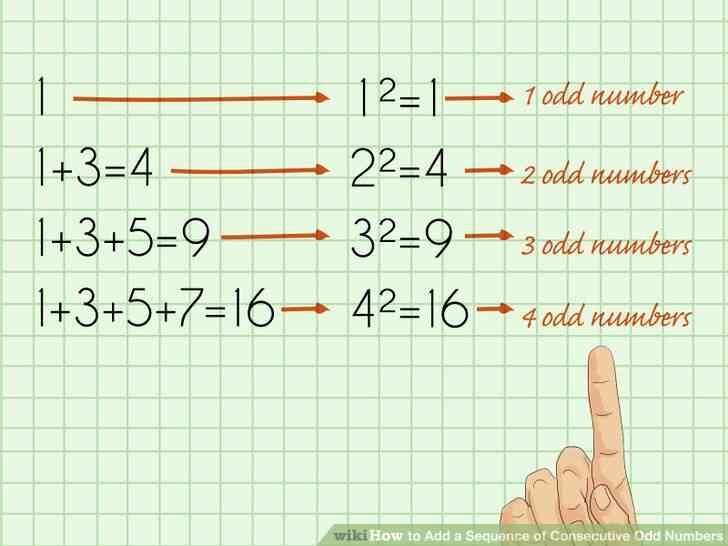
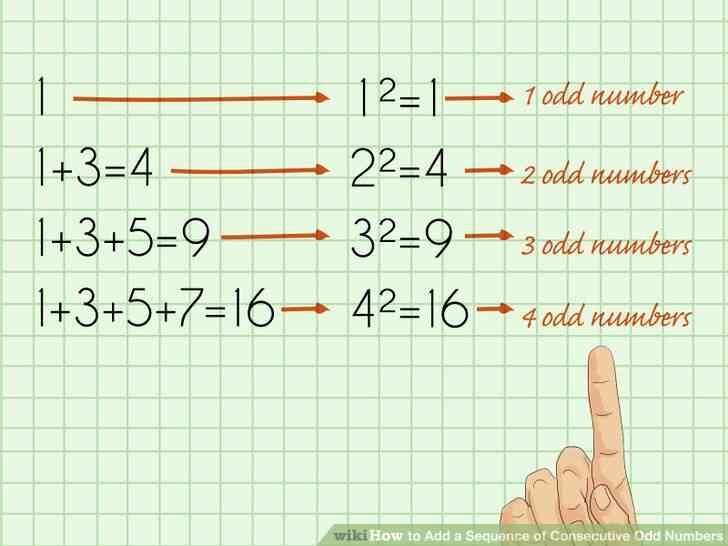
2
@@_
@@Comprendre les donnees provisoires. En resolvant ce probleme, vous avez appris de plus que la somme des nombres. Vous avez egalement appris beaucoup de chiffres consecutifs ont ete ajoutes: 41! C'est parce que le nombre de chiffres additionnes est toujours egale a la racine carree de la somme.
- Somme du premier nombre impair = 1. La racine carree de 1 est 1, et un seul chiffre a ete ajoute.
- Somme des deux premiers nombres impairs = 1 3 = 4. La racine carree de 4 est 2, et les deux chiffres ont ete ajoutes.
- Somme des trois premiers nombres impairs = 1 3 5 = 9. La racine carree de 9 est 3, et les trois chiffres ont ete ajoutes.
- Somme des quatre premiers nombres impairs = 1 3 5 7 = 16. La racine carree de 16 est 4, et quatre chiffres ont ete ajoutes.
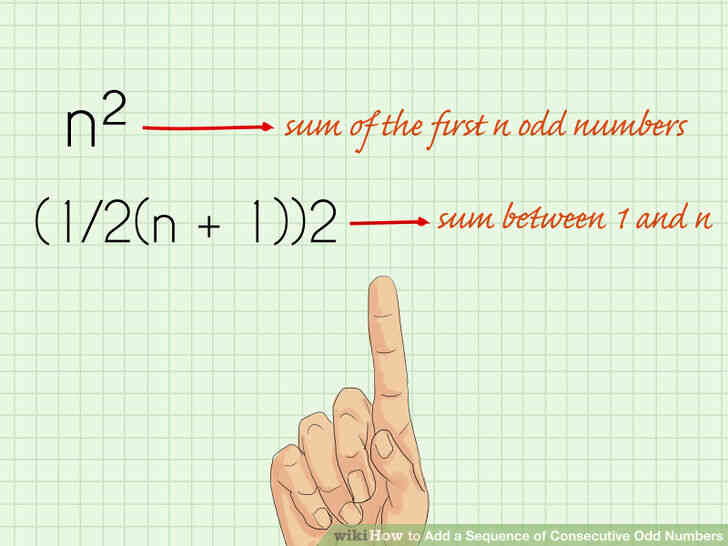
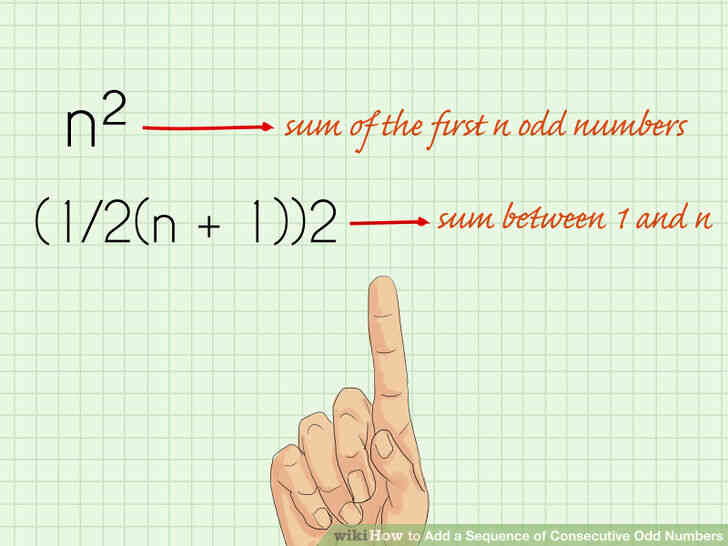
3
@@_
@@Generaliser la formule. Une fois que vous comprenez la formule et comment il fonctionne, vous pouvez l'ecrire dans un format qui leur sera applicable n'importe quel nombre vous avez a faire. La formule pour trouver la somme des n premiers nombres impairs est n x n ou n au carre.
- Par exemple, si vous avez branche 41 pour n, vous auriez 41 x 41 ou 1681, qui est egal a la somme des 41 premiers nombres impairs.
- Si vous ne savez pas combien de numeros vous sont traiter avec, la formule pour determiner la somme entre 1 et n (1/2(n 1))2
@@_
@@
Partie 3
Determiner les Nombres Impairs Consecutifs Ajouter Jusqu'a un Montant


1
@@_
@@Comprendre la difference entre les deux types de problemes. Si vous etes donne une serie de nombres impairs consecutifs et sont invites a trouver leur somme, vous devez utiliser l' (1/2(n 1))2 equation. Si, d'autre part, vous avez reçu une somme et a demande de trouver la serie des nombres impairs consecutifs qui ajoute a cette somme, vous aurez besoin d'utiliser une formule differente tous ensemble.


2
@@_
@@Laissez-n represente le premier numero. Pour trouver ce que les nombres impairs consecutifs ajouter jusqu'a une somme donnee, vous devrez creer une formule algebrique. Commencez par utiliser n pour representer le premier numero de la sequence.[2]


3
@@_
@@Ecrire les nombres restants en termes de n. Ensuite, vous devez determiner comment ecrire le reste des numeros dans l'ordre en termes de n. Parce qu'ils sont tous les nombres impairs consecutifs, il y aura une difference de deux entre chaque numero.
- Cela signifie que le deuxieme numero de la serie n 2, la troisieme sera la n 4, etc.


4
@@_
@@Completer votre formule. Une fois que vous savez comment representer chaque nombre dans la serie, il est temps d'ecrire votre formule. Le cote gauche de votre formule devrait representer les nombres de la serie, et le cote droit devrait representer leur somme.
- Par exemple, si vous avez ete invite a trouver une serie consecutive de deux nombres impairs que d'ajouter jusqu'a 128, on peut ecrire n n 2 = 128.
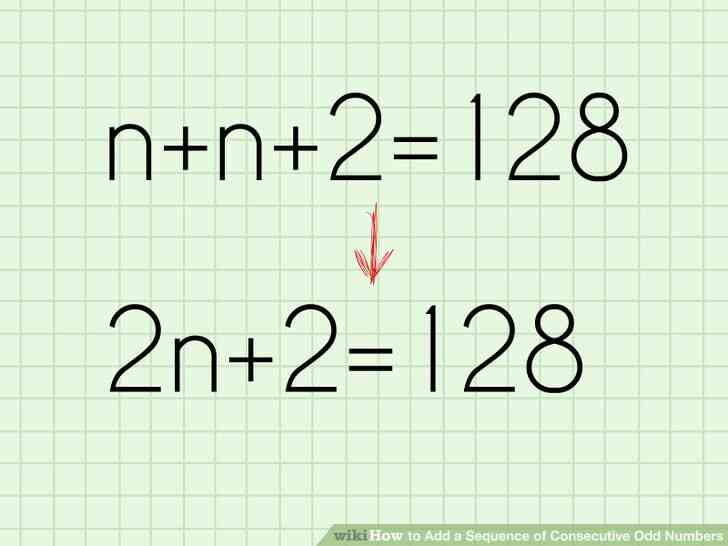
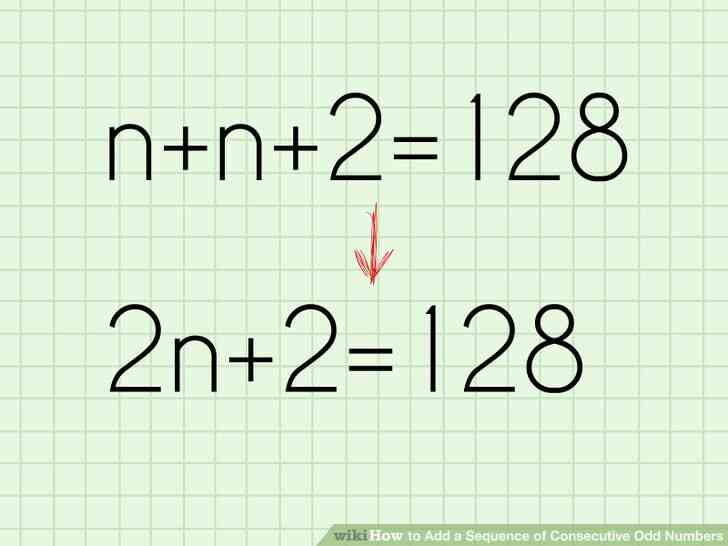
5
@@_
@@Simplifier l'equation. Si vous avez plus d'un n sur le cote gauche de l'equation, ajoutez-les ensemble. Ainsi, il sera beaucoup plus facile a resoudre.
- Par exemple, n n 2 = 128 simplifie a 2n 2 = 128.


6
@@_
@@Isoler n. La derniere etape de la resolution de cette equation est d'obtenir n, par lui-meme sur un cote de l'equation. Rappelez-vous que toutes les modifications que vous apportez a un cote de l'equation, vous devez vous rendre de l'autre cote.
- Traiter avec l'addition et la soustraction de la premiere. Dans ce cas, vous devez soustraire 2 des deux cotes de l'equation pour obtenir n par lui-meme , donc 2n = 126.
- Ensuite traiter avec la multiplication et la division. Dans ce cas, vous avez besoin de diviser les deux cotes par 2 afin d'isoler n, donc n = 113.
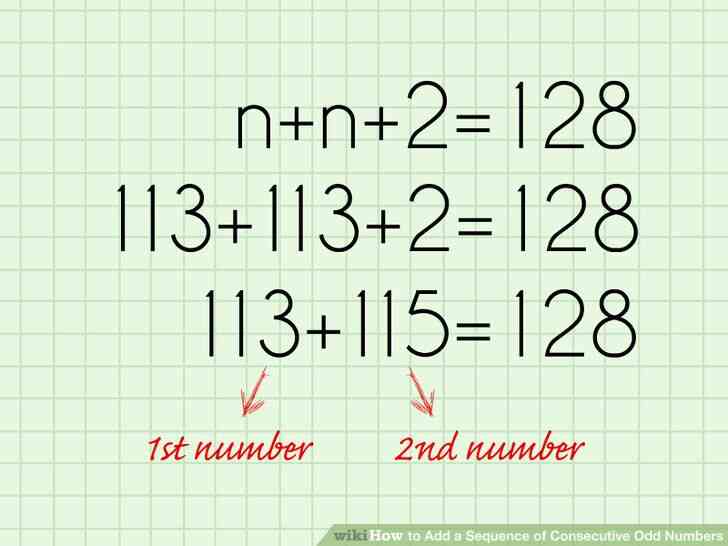
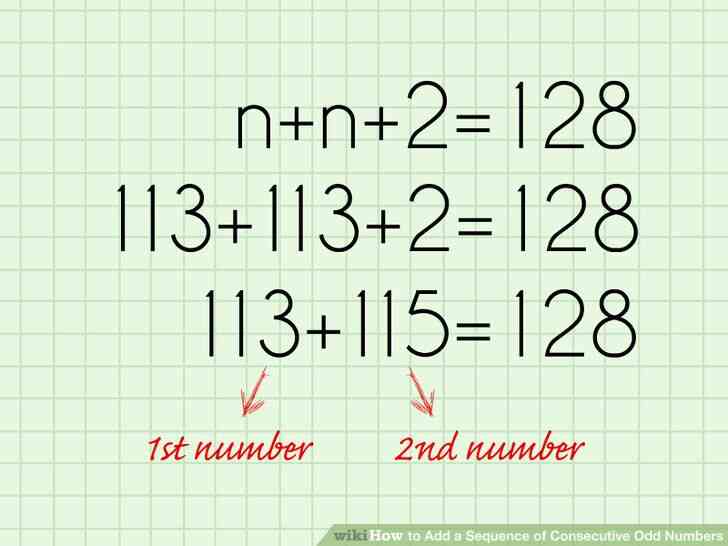
7
@@_
@@Ecrire votre reponse. A ce stade, vous savez que n = 113, mais vous n'etes pas tout a fait fini. Vous devez assurez-vous de repondre entierement a la question qui a ete posee. Si la question vous demande ce que la serie de numeros consecutifs ajoute a une somme donnee, vous devez ecrire tous les nombres.
- La reponse a ce probleme est de 113 et 115 parce que n = 113 et n 2 = 115.
- C'est toujours une bonne idee de verifier votre travail en branchant vos numeros de retour dans l'equation. Si ils ne sont pas egaux a la somme donnee, revenir en arriere et essayer a nouveau.
Comment Ajouter une Séquence de Nombres Impairs Consécutifs
By commentfaire
Vous pouvez ajouter une série de nombres impairs consécutifs à la main, mais il y a un moyen beaucoup plus facile de le faire, surtout si vous avez affaire à un beaucoup de chiffres. Une fois que vous maîtrisez une formule simple, vous serez en mesure d'ajouter ces numéros en un rien de temps, sans utiliser de calculatrice. Il est également un moyen simple pour savoir lequel des nombres consécutifs ajouter jusqu'à une somme donnée.